Alexa告诉我，“意外发现”的定义是“事件以一种愉快或有益的方式偶然发生和发展。”

内容

斯梅尔的生日

正如我之前在这篇博客中提到的，来自安娜堡的Indika Rajapakse，来自伯克利的Stephen Smale和我正在研究一个关于自同步振荡器的Kuramoto模型的项目。史蒂夫的生日在上周，Indika组织了一次Zoom电话会议，有100多名史蒂夫的朋友参加，祝他“生日快乐”。在庆祝活动期间，我发起了与另一位史蒂夫的私人Zoom聊天，来自康奈尔大学的Steven Strogatz，他是Kuramoto的专家。斯特罗加茨和我决定第二天进行一对一的Zoom视频通话。

锁定阈值

我的Kuramoto模拟器使用数值来解仓本方程并研究动力系统的行为。几个月前，我计算了一个叫做锁定阈值对于一个有n个振子的系统。这些值就是图中的圆。我们用$s_n$来表示。

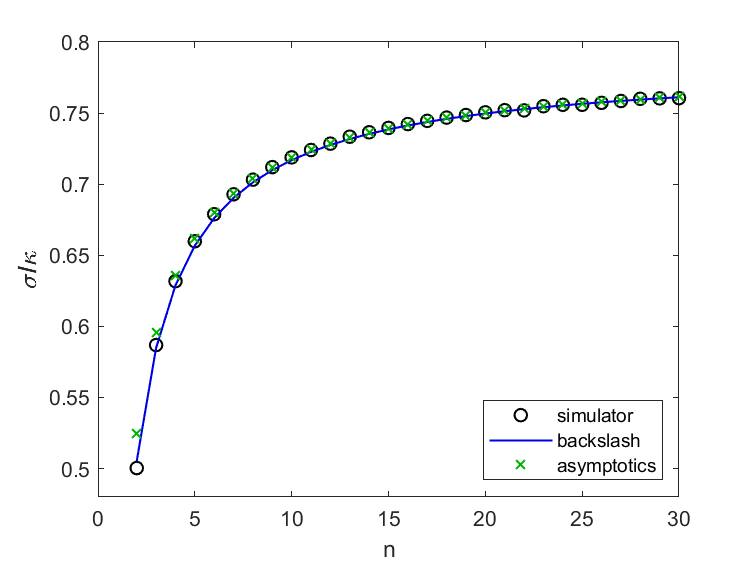
Strogatz渐近分析

在Zoom的通话中，斯特罗加茨向我讲述了他2016年与伯特兰·奥蒂诺-洛夫勒合作的论文，具有均匀频率间隔的仓本模型．在这篇论文中，他们证明了下列令人印象深刻的结果，关于锁阈值的渐近行为是一个$n$的函数。

$ $ \ gamma_L = \压裂{\π}{4}- \压裂n ^{\π}{4}{1}+ 4 \泽塔(- \压裂{1},{2}\压裂{c₁}{2})n ^ {3/2} + O (n ^ {2}) $ $

其中$\zeta(s,q)$是Riemann zeta函数的Hurwitz泛化，$C_1$是David Bailey, Jon Borwein和Richard Crandall在一篇实验数学论文

嗯，我被震住了。$\pi$是从哪里来的?n^{-3/2}$的幂是怎么得到的?赫维茨ζ函数和QRS常数是什么?我无法回答这些问题。

数据符合

我毫不气馁，尝试用这种形式的函数来拟合我的计算值$s_n$

$ $ s_n \大约\压裂{\π}{4}- \压裂n ^{\π}{4}{1}+ c n ^ {3/2} $ $

我发现c = 0.3185，并在图中得到了蓝线。它非常合身。我很兴奋。

意外的惊喜

现在是机缘巧合部分。事实证明我早就知道了戴夫·贝利很长一段时间。他为高性能计算做出了许多贡献，包括令人尊敬的NAS Benchmark。我参加了1993年的会议，当时他和博尔温兄弟乔恩和彼得获得了肖韦内说明文写作奖，表彰他们关于如何计算$\pi$的十亿位数的论文。在那次会议上，鲍温夫妇告诉了我连续六个9在$\pi$的十进制展开的位置780附近。

我还认识理查德·克兰德尔。他是俄勒冈州波特兰市里德学院的教授。他和史蒂夫·乔布斯的交情很长，可以追溯到70年代乔布斯在里德学院读书的时候。实际上，克兰德尔在80年代为我在俄勒冈州比弗顿的英特尔超立方体公司工作时，曾有过一份暑期工作。

渐近

回到仓本，在我完成曲线拟合后，我更仔细地阅读了斯特罗加茨的论文。这是一种熟练而详细的分析，涉及到和收敛到积分。在最后一页，我找到了渐近级数中$n^{-3/2}$项的系数的近似数值，0.3735。这导致了我的图中的绿色x，它惊人地接近于圆圈中的值，因为这个系列的目的是应用为$n \rightarrow \infty$，我从$n = 2$开始计算它。

反斜杠

我怎么计算系数c =。3125?让年代为计算锁定阈值的29 × 1 MATLAB列向量。

S = kuramoto_locking_thresholds;

让n是对应数量的振子的列向量。

N = (2:30)';

然后

T = /4*(1 - 1 /n);

是渐近级数的前两项。也让

P = n.^(-3/2);

我要求出这个标量c这T + c*p是接近于年代越好。这是一个由29个线性方程组成的超定方程组，只有一个未知数。

$$\texttt{p*c} \约\texttt{s-t}$$

如何用MATLAB“求解”这样的方程?最小二乘解用反斜杠计算。

C = p\(s-t)

C = 0.3185

这就得到了图中的蓝线。

拟合= t + c*p;

获取MATLAB代码

发布与MATLAB®R2020b