Alexa告诉我，偶然的定义是“偶然的偶然或有益的方式发生和发展。”

内容

耀眼的生日

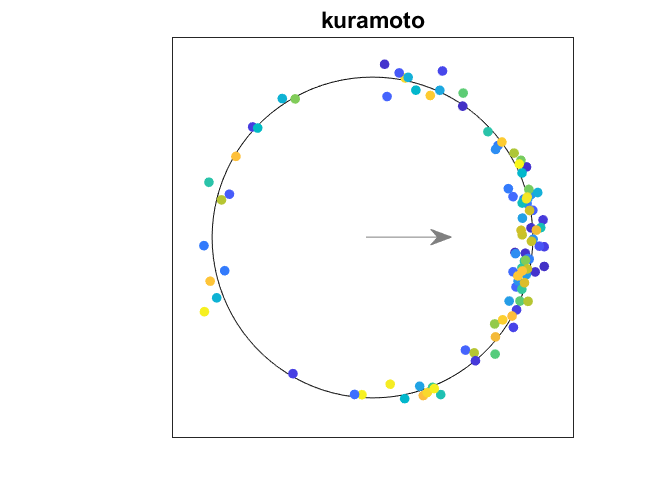
正如我之前提到的那样，来自安娜堡的Indika Rajapakse，来自伯克利的Stephen Smale，我正在研究一个关于自同步振荡器的Kuramoto模型的项目。史蒂夫的生日是上周，Indika组织了一个剧场电话，涉及超过100多个史蒂夫的朋友，祝他“生日快乐”。在庆祝活动期间，我发起了一个私人缩放与另一个史蒂夫，斯蒂芬斯特罗茨从康奈尔举行的私人缩放聊天，他是Kuramoto专家。Strogatz和我决定第二天拥有一对一的缩放视频。

锁定阈值

我的Kuramoto模拟器使用ODE45.解决Kuramoto的方程并调查动态系统的行为。几个月前，我计算了叫做的东西的价值锁定阈值对于一个$n$振荡的系统。这些值就是图中的圆。用$s_n$表示。

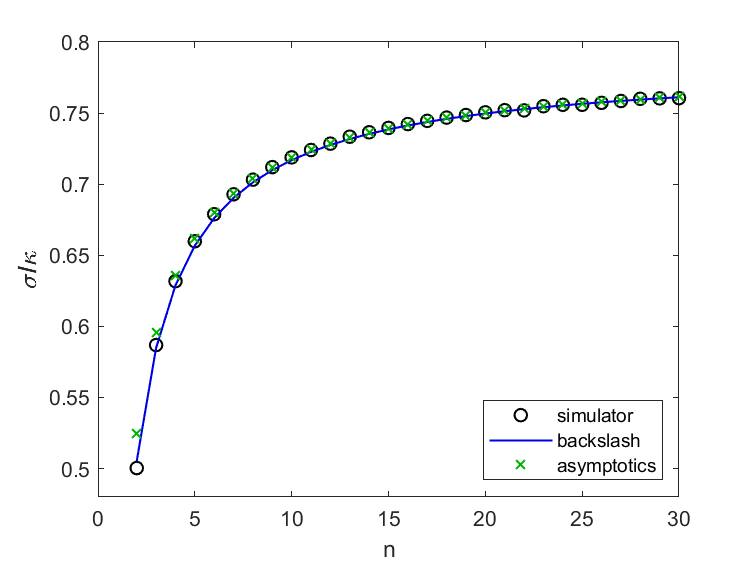
“渐近分析

在与Zoom的通话中，斯特罗加茨告诉了我他在2016年与伯特兰·奥托诺-洛夫勒合著的论文，频率均匀间隔的仓本模型．在本文中，他们证明了锁定阈值的渐近行为的令人印象深刻的结果$ N $的函数。

$$ \ gamma_l = \ frac {\ pi} {4} - \ frac {\ pi} {4} n ^ { - 1} + 4 \ zeta（ - \ frac {1} {2}，\ frac {c_1}{2}）n ^ { - 3/2} + o（n ^ { - 2}）$$

其中$\zeta(s,q)$是Riemann zeta函数的Hurwitz泛化，$C_1$是由David Bailey, Jon Borwein和Richard Crandall in分析的QRS常数实验数学中的一篇论文。

嗯，我被震撼了。那个$\pi$是从哪里来的?幂$n^{-3/2}$是怎么来的?什么是Hurwitz zeta函数和QRS常数?这些问题我一个也答不上来。

数据符合

insunted，我尝试用表单的函数拟合我计算的值$ s_n $

$$ s_n \ inflicat \ frac {\ pi} {4} - \ frac {\ pi} {4} n ^ { - 1} + c n ^ { - 3/2} $$

我发现C = 0.3185以及绘图中产生的蓝线。这是一个美丽的契合。我很兴奋。

意外的惊喜

现在是意外发现的部分。原来我已经知道了戴夫·贝利许久。他对高性能计算作出了许多贡献，包括古老的NAS基准。我在1993年的会议上，当他和彼得·彼得·彼得·彼得（Jon和Peter）收到了Chauvenet奖，即致力于宣传如何计算$ \ PI $的亿位数。在那次会议上，Borwein告诉我了连续六个9大约在$\pi$的小数展开项中的780位置。

我也认识理查德·克兰德尔。他是俄勒冈州波特兰市里德学院的教授。他和史蒂夫·乔布斯有很长一段关系，可以追溯到70年代乔布斯在里德学院(Reed)读书时。事实上，克兰德尔曾为我做过一份暑期工作，当时我在俄勒冈州比弗顿的Intel Hypercube公司工作。

渐近

在完成曲线拟合后，我回到仓本，更仔细地阅读了斯特罗加茨的论文。这是一种巧妙而详细的分析，涉及到和收敛于积分。在最后一页，我找到了渐近级数中$n^{-3/2}$项的系数的近似数值0.3735。这就导致了我的图中的绿色x，它们非常接近圆圈中的值，因为这个系列的目的是作为$n \rightarrow \infty$应用，并且我从$n = 2$开始计算它。

反斜杠

我是怎么计算系数c =。3125的?让年代为计算锁定阈值的29 × 1 MATLAB列向量。

s = kuramoto_locking_thresholds;

让n是相应振子数的列向量。

n =(2)”;

然后

T = /4*(1 - 1 /n);

是渐近级数的前两项。也让

p = n。^ (3/2);

我想找到标量c这t + c * p是接近吗年代越好。这是一个29个线性方程组的超定方程组，只有一个未知数。

$$ \ texttt {p * c} \ attum \ texttt {s-t} $$

你如何用matlab“解决”这样的等式？最小二乘解决方案由反斜杠计算。

c = p \（s-t）

C = 0.3185.

这是图中蓝色的线。

fit = t + c * p;

获取matlab代码

发布与MATLAB®R2020B