Alexa告诉我，偶然性的定义是“以幸福或有益的方式偶然发生事件的发生和发展”。

内容

Smale生日

正如我之前在此博客中提到的，Ann Arbor的Indika Rajapakse，来自伯克利的Stephen Smale和我正在研究一个有关库拉莫托自同步振荡器模型的项目。史蒂夫（Steve）的生日是上周，Indika组织了一个Zoom电话会议，涉及100多个史蒂夫（Steve）的朋友，祝他“生日快乐”。在庆祝活动中，我与库拉马托专家康奈尔的另一位史蒂夫·斯特罗加兹（Steven Strogatz）进行了私人缩放聊天。Strogatz和我决定第二天进行一对一的变焦视频。

Locking Threshold

My Kuramoto simulator usesODE45求解库拉莫托方程并研究动力系统的行为。几个月前，我计算了所谓的事物的值locking thresholdfor a system of $n$ oscillators. These values are the circles in this plot. Let's denote them by $s_n$.

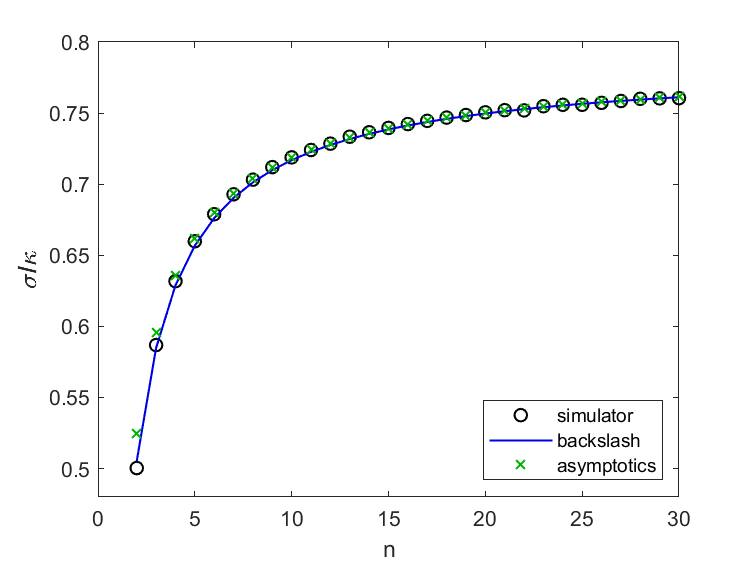
Strogatz asymptotic analysis

In our Zoom call, Strogatz told me about his 2016 paper with Bertrand Ottino-Loffler,Kuramoto model with uniformly spaced frequencies。在本文中，他们证明了以下令人印象深刻的结果，即锁定阈值的渐近行为$ n $。

$ \ gamma_l = \ frac {\ pi} {4} - \ frac {\ pi} {4} n^{ - 1} + 4 \ zeta（ - \ frac {1} {1} {2} {2}，\ frac {c_1}}{2}）n^{ - 3/2} + o（n^{ - 2}）$$

where $\zeta(s,q)$ is the Hurwitz generalization of the Riemann zeta function and $C_1$ is the QRS constant analyzed by David Bailey, Jon Borwein and Richard Crandall ina paper in Experimental Mathematics.

Well, I was blown away. Where did that $\pi$ come from? How did the power $n^{-3/2}$ get there? What are the Hurwitz zeta function and the QRS constant? I couldn't answer any of these questions.

Data fit

毫无疑问，我尝试将计算值$ s_n $与表格的函数拟合

$$ s_n \ oft \ frac {\ pi} {4} - \ frac {\ pi} {4} n^{ - 1} + c n^{ - 3/2} $ 4

我发现c = 0.3185和图中所得的蓝线。这是一个美丽的健康。我很兴奋。

Serendipity

Now the serendipity part. It turns out that I've knownDave Baileyfor a long time. He has made numerous contributions to high performance computing, including the venerable NAS Benchmark. I was at the 1993 meeting when he and the Borwein brothers, Jon and Peter, received the Chauvenet Prize for expository writing honoring their paper about how to compute a billion digits of $\pi$. At that meeting, the Borwein's told me about the连续六个9saround location 780 in the decimal expansion of $\pi$.

I also knew Richard Crandall. He was a professor at Reed College in Portland, Oregon. He had a long association with Steve Jobs, dating back to Jobs' stint as a student at Reed in the '70s. Crandall actually had a summer job working for me when I was at the Intel Hypercube operation in Beaverton, Oregon in the '80s.

Asymptotics

Getting back to Kuramoto, after I had done my curve fit, I read the Strogatz paper more thoroughly. It is a skillful and detailed analysis involving sums converging to integrals. On the last page I found the approximate numerical value, 0.3735, for the coefficient of the $n^{-3/2}$ term in the asymptotic series. That leads to the green x's in my plot, which are amazingly close to the values in the circles since the series is intended to apply as $n \rightarrow \infty$ and I am evaluating it starting with $n = 2$.

Backslash

How did I compute the coefficient c = .3125? Letsbe the 29-by-1 MATLAB column vector of computed locking thresholds.

s = kuramoto_locking_thresholds;

让nbe the column vector of corresponding number of oscillators.

n = (2:30)';

Then

t = pi/4*(1 - 1./n);

is the first two terms in the asymptotic series. Also let

p = n.^(-3/2);

我想找到标量cso thatt + c*pis as close as tosas possible. This an overdetermined system of 29 linear equations with only one unknown.

$$ \ texttt {p*c} \ about texttt {s-t} $$

您如何使用MATLAB“解决”这样的方程式？最小二乘解决方案是通过后斜杠计算的。

c = p\(s-t)

C = 0.3185

This gives me the blue line in the graphic.

fit = t + c*p;

获取MATLAB代码

与Matlab®R2020B一起出版