我很惊讶当许多的非对称变体希尔伯特矩阵的奇异值是几乎等于\π美元。解释涉及一个方波的傅里叶级数。

内容

非对称希尔伯特矩阵

我的第一个项目在矩阵计算涉及到希尔伯特矩阵。它在1894年推出的著名数学家大卫希尔伯特作为我们今天所谓的正规方程系数矩阵的多项式最小二乘近似的单项基础。的元素n——- n美元美元希尔伯特矩阵

$ $现代{i, j} = \压裂{1}{我+ j - 1}, \ \我,j = 1,……n $ $

几年前,我想要一个非对称矩阵测试,所以我改变了分母的加号减号,但是这些元素沿着副斜杆炸毁了,所以我也改变了1 + 1/2。

$ $现代{i, j} = \压裂{1},{i j + 1/2} \ \ i, j = 1,……n $ $

我称之为非对称希尔伯特矩阵。这是5-by-5格式的老鼠。

格式老鼠n = 5;(I, J) = ndgrid (1: n);一个= 1. / (i j + 1/2)

2 = 2 2/3 2/3 2 2 2/3 -2/5 2/5 -2/7 -2/5 2/3 2 2 2/3 2/3 2 2 2/9 2/7 2/5 2/7 2/5 2/3 2

奇异值

我吃惊的是当我碰巧计算奇异值。下面是所有的奇异值30-by-30非对称希尔伯特矩阵。

格式长n = 30;(I, J) = ndgrid (1: n);一个= 1. / (i j + 1/2);σ=圣言(A)

σ= 3.141592653589795 3.141592653589794 3.141592653589794 3.141592653589794 3.141592653589794 3.141592653589794 3.141592653589793 3.141592653589793 3.141592653589793 3.141592653589793 3.141592653589793 3.141592653589792 3.141592653589792 3.141592653589792 3.141592653589791 3.141592653589779 3.141592653589737 3.141592653588278 3.141592653559363 3.141592653039148 3.141592644613932 3.141592521935767 3.141590919627153 3.141572215205717 3.141378147613475 3.139604197477250 3.125546289482884 3.032461817019588 2.564498174433655 1.105241141304968

难以置信的是,其中一半是相等的π我们长期的完整格式,这是16位数。但过去几等于π至少两位数。这是怎么发生的呢?

高精度计算

再次让我们做30-by-30圣言,这次使用符号工具箱和100 -位的算术。计算需要大约一分半钟在我的机器上。

抽搐的数字(100)n = 30;(I, J) = ndgrid(信谊(1:n));一个= 1. / (i j + 1/2);σ=圣言();toc

运行时间是83.939032秒。

这是第一个奇异值,100位。

sigma1 =σ(1)

sigma1 = 3.141592653589793238462643383279502884197169352107009745551549597527462440105298598090594765999823398

这里是一个对数图之间的区别\π美元和奇异值。

semilogy (abs(π-σ),“。”)包含(“n”)ylabel (“| \π- \σ|”);

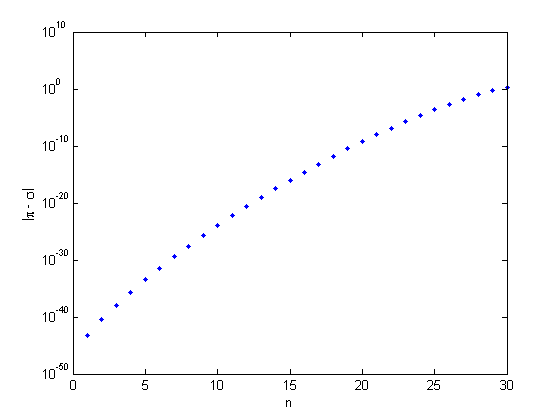
第一个奇异值= \π44位,美元作为我们的双精度计算预测,十五的三十奇异值等于\π美元至少15位数。

西摩合作者

西摩合作者是斯坦福大学客座教授当我还是一个研究生在1960年代早期。我一个人在他的监督下阅读课程。他从斯坦福大学的威斯康辛州,在那里他度过了他的职业生涯作为一个数学和计算机科学的教授。他是总统的暹罗在1981年和82年。

1985年,第二个暹罗会议上线性代数在罗利北卡罗来纳州立大学举行。我演示了MATLAB在喝咖啡。我们没有展位,只是一个书桌或桌子上。我用这个例子示范,要求与会人员,如果他们可以解释\π美元的外观。西摩说他可以。他写的两篇论文20年前的托普利兹矩阵特征值相关。他很快就产生了另一篇论文,引用下面解释的行为我非对称希尔伯特的奇异值矩阵。相关结果从1920年由著名的匈牙利数学家伽柏Szego。

托普利兹矩阵

矩阵是常数沿对角线美元美元,所以这是一个托普利兹矩阵。所以是2美元n——- 2 n矩阵B美元美元由美元美元的MATLAB数组操作

Z = 0(大小(A));B = - * [Z;——“0);

在埃尔米特和托普利兹矩阵B美元。它的特征值是真实发生在+ / -对。特征值的绝对值B美元的奇异值一美元,每个重复两次。

Szego 1920定理说,托普利兹矩阵的特征值由一个函数的傅里叶展开的系数收敛到该函数的最大值和最小值。

参与者意识到两个重要的事实。首先,他可以分析非对称矩阵的奇异值一美元通过观察埃尔米特矩阵的特征值B美元。第二,美元和美元B美元的元素是奇数的倒数,即一个方波的傅里叶展开的系数。所以Szego是1920定理意味着B,因此美元的最大特征值的最大奇异值一美元收敛于最大的方波。

方波

已经有一个提示是怎么回事老MATLAB演示命名xfourier。的第一行xfourier说

这个例子展示了(图形)方波的傅里叶级数展开由奇数次谐波之和。

的核心xfourier是一个类似的代码片段。

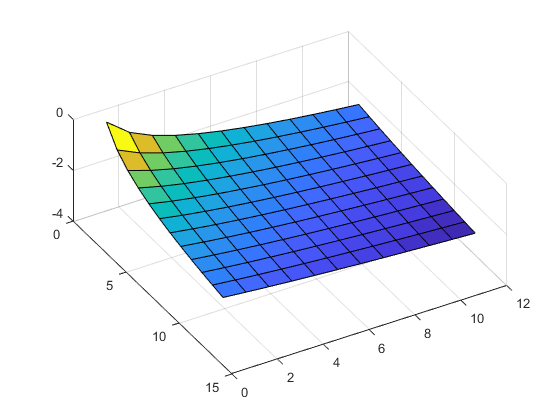
t = -ππ/ 256:π;y = 0(大小(t));为k = 1:2:99 y = y +罪(k * t) / k;结束情节(t, y)

情节展示了两件事。首先注意到过度的间隔称为吉布斯现象。但更重要的是对我们来说这是收敛的室内间隔值+和- 0.8附近。

让我们用更多的条款和仔细看看。

t = -ππ/ 256:π;y = 0(大小(t));为k = 1:2:599 y = y +罪(k * t) / k;结束情节(t, y)轴([0π结果.76])

我们找到融合点态值接近0.7854。代码片段近似傅立叶正弦扩张

$ $ s (t) = \ sum_ {k奇怪\}\压裂{罪\ {kt}} {k} $ $

系数的倒数是奇数,是一样的非对称希尔伯特的元素矩阵。

傅里叶级数收敛点态\ \下午π/ 4美元。如果我们跟踪这个事实通过参与者的分析和Szego定理,我们有一个解释,非对称希尔伯特矩阵的最大奇异值收敛\π美元。

e . e . Tyrtyshnikov

Evgenij大肠Tyrtyshnikov教授和数值数学研究所副主任在莫斯科的俄罗斯科学院。1991年,他研究了这个矩阵的奇异值小的行为。1992年,他认为1/2的矩阵是任何noninteger值所取代。

引用

西摩诉合作者,托普利兹矩阵的奇异值的分布,线性代数及其应用80,1986,115 - 130,< http://www.sciencedirect.com/science/article/pii/0024379586902806>

Evgenij e . Tyrtyshnikov Cauchy-Toeplitz矩阵和某些应用程序中,线性代数及其应用149、1991队,< http://www.sciencedirect.com/science/article/pii/002437959190321M>

Evgenij e . Tyrtyshnikov cauchy-toeplitz矩阵的奇异值,线性代数及其应用161,1992,99 - 116,< http://www.sciencedirect.com/science/article/pii/002437959290007W>

得到了MATLAB代码

发表与MATLAB®R2014a

发表与MATLAB®R2014a