主要内容
胆固醇
柯列斯基分解
描述
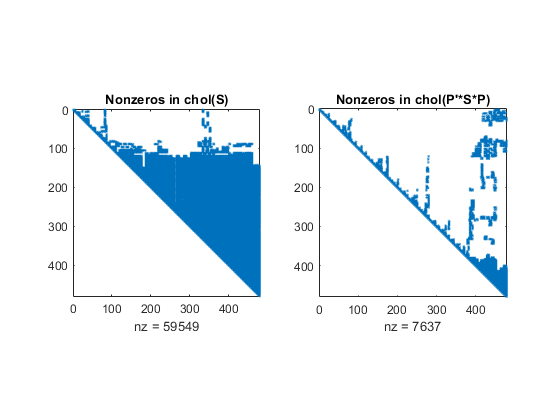
[指定是否返回排列信息R,国旗,P) =胆固醇(___,outputForm)P作为矩阵或向量,使用前面语法中的任何输入参数组合。此选项仅适用于稀疏矩阵输入。例如,如果outputForm是“向量”和国旗= 0,然后年代(p, p) = R * R.的默认值outputForm是“矩阵”这样‘* R = P ' S * P.
例子
输入参数
输出参数
更多关于
提示
使用
胆固醇(而不是eig)来有效地确定一个矩阵是否对称正定。看到确定矩阵是否对称正定为更多的信息。
扩展功能
之前介绍过的R2006a