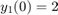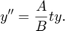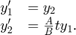Main Content

ode23t

Solve moderately stiff ODEs and DAEs — trapezoidal rule

collapse all in page

Syntax

[t,y] = ode23t(odefun,tspan,y0)
[t,y] = ode23t(odefun,tspan,y0,options)
[t,y,te,ye,ie] = ode23t(odefun,tspan,y0,options)
sol = ode23t(___)

Description

example

[t,y] = ode23t(odefun,tspan,y0), wheretspan = [t0 tf], integrates the system of differential equations y ' = f ( t , y ) fromt0totfwith initial conditionsy0。Each row in the solution arrayycorresponds to a value returned in column vectort。

All MATLAB®ODE solvers can solve systems of equations of the form y ' = f ( t , y ) , or problems that involve a mass matrix, M ( t , y ) y ' = f ( t , y ) 。解决所有使用类似的语法。的ode23ssolver only can solve problems with a mass matrix if the mass matrix is constant.ode15sandode23tcan solve problems with a mass matrix that is singular, known as differential-algebraic equations (DAEs). Specify the mass matrix using theMassoption ofodeset。

example

[t,y] = ode23t(odefun,tspan,y0,options)also uses the integration settings defined byoptions, which is an argument created using theodesetfunction. For example, use theAbsTolandRelToloptions to specify absolute and relative error tolerances, or theMassoption to provide a mass matrix.

[t,y,te,ye,ie] = ode23t(odefun,tspan,y0,options)additionally finds where functions of(t,y), called event functions, are zero. In the output,teis the time of the event,yeis the solution at the time of the event, andieis the index of the triggered event.

For each event function, specify whether the integration is to terminate at a zero and whether the direction of the zero crossing matters. Do this by setting the'Events'property to a function, such asmyEventFcnor@myEventFcn, and creating a corresponding function: [value,isterminal,direction] =myEventFcn(t,y). For more information, seeODE Event Location。

sol= ode23t(___)returns a structure that you can use withdevalto evaluate the solution at any point on the interval[t0 tf]。You can use any of the input argument combinations in previous syntaxes.

Examples

collapse all

Open Live Script

Simple ODEs that have a single solution component can be specified as an anonymous function in the call to the solver. The anonymous function must accept two inputs(t,y), even if one of the inputs is not used in the function.

Solve the ODE

y ′ = - 1 0 t 。

Specify a time interval of[0 2]and the initial conditiony0 = 1。

tspan = [0 2]; y0 = 1; [t,y] = ode23t(@(t,y) -10*t, tspan, y0);

Plot the solution.

plot(t,y,'-o')

Figure contains an axes object. The axes object contains an object of type line.

Open Script

An example of a stiff system of equations is the van der Pol equations in relaxation oscillation. The limit cycle has regions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff.

的system of equations is:

数组$ $ \开始{}{cl} y_1 ' & # 38; =y_2\\y_2' &= 1000(1-y_1^2)y_2-y_1\end{array}$$

的initial conditions are$y_1(0)=2$and$y_2(0)=0$。的functionvdp1000ships with MATLAB® and encodes the equations.

functiondydt = vdp1000(t,y)%VDP1000 Evaluate the van der Pol ODEs for mu = 1000.%% See also ODE15S, ODE23S, ODE23T, ODE23TB.% Jacek Kierzenka and Lawrence F. Shampine% Copyright 1984-2014 The MathWorks, Inc.dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];

Solving this system usingode45with the default relative and absolute error tolerances (1e-3and1e-6, respectively) is extremely slow, requiring several minutes to solve and plot the solution.ode45requires millions of time steps to complete the integration, due to the areas of stiffness where it struggles to meet the tolerances.

This is a plot of the solution obtained byode45, which takes a long time to compute. Notice the enormous number of time steps required to pass through areas of stiffness.

Solve the stiff system using theode23tsolver, and then plot the first column of the solutionyagainst the time pointst。的ode23tsolver passes through stiff areas with far fewer steps thanode45。

[t,y] = ode23t(@vdp1000,[0 3000],[2 0]); plot(t,y(:,1),'-o')

Open Script

ode23tonly works with functions that use two input arguments,tandy。不过,您可以通过在def额外参数ining them outside the function and passing them in when you specify the function handle.

Solve the ODE

$$y'' = \frac{A}{B} t y.$$

Rewriting the equation as a first-order system yields

$$\begin{array}{cl} y'_1 &= y_2\\ y'_2 &= \frac{A}{B} t y_1. \end{array}$$

odefcn.mrepresents this system of equations as a function that accepts four input arguments:t,y,A, andB。

functiondydt = odefcn(t,y,A,B) dydt = zeros(2,1); dydt(1) = y(2); dydt(2) = (A/B)*t.*y(1);

Solve the ODE usingode23t。Specify the function handle such that it passes in the predefined values forAandBtoodefcn。

A = 1; B = 2; tspan = [0 5]; y0 = [0 0.01]; [t,y] = ode23t(@(t,y) odefcn(t,y,A,B), tspan, y0);

Plot the results.

plot(t,y(:,1),'-o',t,y(:,2),'-.')

Open Live Script

的ode15ssolver is a good first choice for most stiff problems. However, the other stiff solvers might be more efficient for certain types of problems. This example solves a stiff test equation using all four stiff ODE solvers.

Consider the test equation

y ′ = - λ y 。

的equation becomes increasingly stiff as the magnitude of λ increases. Use λ = 1 × 1 0 9 and the initial condition y ( 0 ) = 1 over the time interval[0 0.5]。With these values, the problem is stiff enough thatode45andode23struggle to integrate the equation. Also, useodesetto pass in the constant Jacobian J = ∂ f ∂ y = - λ and turn on the display of solver statistics.

lambda = 1e9; y0 = 1; tspan = [0 0.5]; opts = odeset('Jacobian',-lambda,'Stats','on');

Solve the equation withode15s,ode23s,ode23t, andode23tb。Make subplots for comparison.

subplot(2,2,1) tic, ode15s(@(t,y) -lambda*y, tspan, y0, opts), toc
104 successful steps 1 failed attempts 212 function evaluations 0 partial derivatives 21 LU decompositions 210 solutions of linear systems Elapsed time is 1.505900 seconds.
title('ode15s') subplot(2,2,2) tic, ode23s(@(t,y) -lambda*y, tspan, y0, opts), toc
63 successful steps 0 failed attempts 191 function evaluations 0 partial derivatives 63 LU decompositions 189 solutions of linear systems Elapsed time is 0.439813 seconds.
title('ode23s') subplot(2,2,3) tic, ode23t(@(t,y) -lambda*y, tspan, y0, opts), toc
95 successful steps 0 failed attempts 125 function evaluations 0 partial derivatives 28 LU decompositions 123 solutions of linear systems Elapsed time is 0.598499 seconds.
title('ode23t') subplot(2,2,4) tic, ode23tb(@(t,y) -lambda*y, tspan, y0, opts), toc
71 successful steps 0 failed attempts 167 function evaluations 0 partial derivatives 23 LU decompositions 236 solutions of linear systems Elapsed time is 0.600518 seconds.
title('ode23tb')

Figure contains 4 axes objects. Axes object 1 with title ode15s contains 2 objects of type line. Axes object 2 with title ode23s contains 2 objects of type line. Axes object 3 with title ode23t contains 2 objects of type line. Axes object 4 with title ode23tb contains 2 objects of type line.

的stiff solvers all perform well, butode23scompletes the integration with the fewest steps and runs the fastest for this particular problem. Since the constant Jacobian is specified, none of the solvers need to calculate partial derivatives to compute the solution. Specifying the Jacobian benefitsode23sthe most since it normally evaluates the Jacobian in every step.

For general stiff problems, the performance of the stiff solvers varies depending on the format of the problem and specified options. Providing the Jacobian matrix or sparsity pattern always improves solver efficiency for stiff problems. But since the stiff solvers use the Jacobian differently, the improvement can vary significantly. Practically speaking, if a system of equations is very large or needs to be solved many times, then it is worthwhile to investigate the performance of the different solvers to minimize execution time.

Input Arguments

collapse all

Functions to solve, specified as a function handle that defines the functions to be integrated.

的functiondydt = odefun(t,y), for a scalartand a column vectory, must return a column vectordydtof data typesingleordoublethat corresponds to f ( t , y ) 。odefunmust accept both input argumentstandy, even if one of the arguments is not used in the function.

For example, to solve y ' = 5 y − 3 , use the function:

functiondydt = odefun(t,y) dydt = 5*y-3;end

For a system of equations, the output ofodefunis a vector. Each element in the vector is the solution to one equation. For example, to solve

y ' 1 = y 1 + 2 y 2 y ' 2 = 3 y 1 + 2 y 2

use the function:

functiondydt = odefun(t,y) dydt = zeros(2,1); dydt(1) = y(1)+2*y(2); dydt(2) = 3*y(1)+2*y(2);end

For information on how to provide additional parameters to the functionodefun, seeParameterizing Functions。

Example:@myFcn

Data Types:function_handle

Interval of integration, specified as a vector. At a minimum,tspanmust be a two-element vector[t0 tf]specifying the initial and final times. To obtain solutions at specific times betweent0andtf, use a longer vector of the form[t0,t1,t2,...,tf]。的elements intspanmust be all increasing or all decreasing.

的solver imposes the initial conditions given byy0at the initial timetspan(1), and then integrates fromtspan(1)totspan(end):

  • Iftspanhas two elements[t0 tf], then the solver returns the solution evaluated at each internal integration step within the interval.

  • Iftspanhas more than two elements[t0,t1,t2,...,tf], then the solver returns the solution evaluated at the given points. However, the solver does not step precisely to each point specified intspan。Instead, the solver uses its own internal steps to compute the solution, and then evaluates the solution at the requested points intspan。的solutions produced at the specified points are of the same order of accuracy as the solutions computed at each internal step.

    Specifying several intermediate points has little effect on the efficiency of computation, but can affect memory management for large systems.

的values oftspanare used by the solver to calculate suitable values forInitialStepandMaxStep:

  • Iftspancontains several intermediate points[t0,t1,t2,...,tf], then the specified points give an indication of the scale for the problem, which can affect the value ofInitialStep解算器使用。因此,解决方案获得ed by the solver might be different depending on whether you specifytspanas a two-element vector or as a vector with intermediate points.

  • 的initial and final values intspanare used to calculate the maximum step sizeMaxStep。的refore, changing the initial or final values intspancan cause the solver to use a different step sequence, which might change the solution.

Example:[1 10]

Example:[1 3 5 7 9 10]

Data Types:single|double

Initial conditions, specified as a vector.y0must be the same length as the vector output ofodefun, so thaty0contains an initial condition for each equation defined inodefun。

Data Types:single|double

Option structure, specified as a structure array. Use theodesetfunction to create or modify theoptionsstructure. SeeSummary of ODE Optionsfor a list of the options compatible with each solver.

Example:options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot)specifies a relative error tolerance of1e-5, turns on the display of solver statistics, and specifies the output function@odeplotto plot the solution as it is computed.

Data Types:struct

Output Arguments

collapse all

Evaluation points, returned as a column vector.

  • Iftspancontains two elements[t0 tf], thentcontains the internal evaluation points used to perform the integration.

  • Iftspancontains more than two elements, thentis the same astspan。

Solutions, returned as an array. Each row inycorresponds to the solution at the value returned in the corresponding row oft。

Time of events, returned as a column vector. The event times intecorrespond to the solutions returned inye, andiespecifies which event occurred.

Solution at time of events, returned as an array. The event times intecorrespond to the solutions returned inye, andiespecifies which event occurred.

Index of triggered event function, returned as a column vector. The event times intecorrespond to the solutions returned inye, andiespecifies which event occurred.

Structure for evaluation, returned as a structure array. Use this structure with thedevalfunction to evaluate the solution at any point in the interval[t0 tf]。的solstructure array always includes these fields:

Structure Field Description

sol.x

Row vector of the steps chosen by the solver.

sol.y

Solutions. Each columnsol.y(:,i)contains the solution at timesol.x(i)。

sol.solver

Solver name.

Additionally, if you specify theEventsoption ofodesetand events are detected, thensolalso includes these fields:

Structure Field Description

sol.xe

Points when events occurred.sol.xe(end)contains the exact point of a terminal event, if any.

sol.ye

Solutions that correspond to events insol.xe。

sol.ie

Indices into the vector returned by the function specified in theEventsoption. The values indicate which event the solver detected.

Algorithms

ode23tis an implementation of the trapezoidal rule using a “free” interpolant. This solver is preferred overode15sif the problem is only moderately stiff and you need a solution without numerical damping.ode23talso can solve differential algebraic equations (DAEs)[1],[2]。

References

[1] Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, “Solving Index-1 DAEs in MATLAB and Simulink”,SIAM Review, Vol. 41, 1999, pp. 538–552.

[2] Shampine, L. F. and M. E. Hosea, “Analysis and Implementation of TR-BDF2,”Applied Numerical Mathematics 20, 1996.

See Also

|||

Topics

Introduced before R2006a

MATLAB Documentation

金宝app

Introducing Deep Learning with MATLAB

Introducing Deep Learning with MATLAB

Download ebook