T-SNE.
什么是t-sne?
t-sne(tsne)是一种非常适合于可视化高维数据的降维算法。这个名字代表t-分布式随机邻居嵌入。其思想是将高维点嵌入到低维中,同时考虑点之间的相似性。高维空间中的近点对应于附近嵌入的低维点,高维空间中的远点对应于远处嵌入的低维点。(通常,不可能精确匹配高维和低维空间之间的距离。)
的tsne函数从高维数据创建一组低维点。通常,您可以可视化低维点,以查看原始高维数据中的自然集群。
该算法采用以下一般步骤来嵌入低维度的数据。
计算高维点之间的成对距离。
创建一个标准偏差σ我对于每个高维点我这样困惑每个点都在一个预定的水平。关于困惑的定义,请看计算距离,高斯差异和相似之处.
计算相似性矩阵.这是X的联合概率分布,由方程1.
创建初始的低维点集。
迭代地更新低维点,以最小化高尺空间中高斯分布之间的kullback-leibler发散t在低维空间中的分布。这个优化过程是算法中最耗时的部分。
去找范德马顿和辛顿[1].
t-SNE算法
基本T-SNE算法执行以下步骤。
准备数据
tsne首先删除包含任意的输入数据X的每一行南值。然后,如果标准化名称值对是真的,tsne通过减去每列的平均值来递减X,并通过标准偏差除以列来缩放X。
最初的作者范德马顿和辛顿[1]建议将原始数据x减少到低维版本主成分分析(PCA).你可以设置tsnenumpcacomomonents.名称-值对的维度数,可能是50。要对这一步进行更多的控制,可以使用主成分分析函数。
计算距离,高斯差异和相似之处
预处理后,tsne计算距离d(x我,xj)每对点之间x我和xj在x中,您可以使用距离名称-值对。默认情况下,tsne使用标准欧几里德公制。tsne在其后续计算中使用距离度量的平方。
然后为每一行我(X)tsne计算标准偏差σ我这样困惑的行我等于困惑名称-值对。perplexity是用模型高斯分布定义的,如下所示。范德马顿和辛顿[1]描述,“数据点的相似性xj到数据点x我为条件概率,
,这x我会选择xj作为它的邻居,如果邻居是根据它们的概率密度在高斯中心x我.对于附近的数据点,
相对较高,而对于广泛分离的数据点,
几乎是无穷小的(对于高斯分布方差的合理值,σ我)。”
定义的条件概率j给予我作为
然后定义联合概率pij通过对称条件概率:
| (1) |
在哪里N是X的行数。
这些分布仍然没有标准差σ我定义为困惑名称-值对。让P我表示给定数据点的所有其他数据点的条件概率分布x我.分布的复杂之处在于
在哪里H(P我)Shannon熵是P我:
复杂度度量的是点的有效邻域数我.tsne对象上执行二进制搜索σ我为每一点实现一个固定的困惑我.
初始化嵌入和散度
为了将X中的点嵌入低维空间,tsne执行优化。tsne试图最小化X和一个学生点的模型高斯分布之间的Kullback-Leibler发散t点Y在低维空间中的分布。
最小化过程从一个初始点Y集合开始。tsne默认情况下创建随机高斯分布点。你也可以自己创建这些点,并将它们包含在'initialy'名称 - 值对tsne.tsne然后计算Y中每对点之间的相似性。
的概率模型问ij点之间的距离分布y我和yj是
利用这个定义和X中的距离模型方程1,Kullback-Leibler在联合分布之间发散P和问是
关于这个定义的结果,请参见有用的非线性失真.
Kullback-Leibler散度的梯度下降
尽量减少kullback-leibler发散,即'精确的'算法采用改进的梯度下降过程。散度在Y上的梯度是
归一化术语的地方
改进的梯度下降算法使用了一些调整参数,试图达到一个良好的局部最小值。
t-SNE的Barnes-Hut变异
加快T-SNE算法并减少其内存使用情况,tsne提供近似优化方案。Barnes-Hut算法在一起的算法组在一起,以降低T-SNE优化步骤的复杂性和内存使用情况。Barnes-Hut算法是一个近似优化器,而不是精确的优化器。有一个非负调整参数θ.这影响了速度和准确性之间的权衡。更大的值“θ”给出更快但不太准确的优化结果。该算法对算法相对不敏感“θ”范围内的值(0.2,0.8)。
Barnes-HUT算法在低维空间中附近的算法组,并基于这些组执行近似梯度下降。最初用于天体物理学的想法是梯度与附近点相似,因此可以简化计算。
见Van der Maaten[2].
t-SNE的特点
不能使用嵌入来对新数据进行分类
因为T-SNE经常将数据集群分开,因此T-SNE可以对新数据点进行分类。但是,T-SNE无法分类新点。T-SNE嵌入是一个非线性映射,它依赖于数据。要在低维空间中嵌入新的点,您无法使用以前的嵌入作为地图。相反,再次运行整个算法。
性能取决于数据大小和算法
t-SNE处理数据需要很长时间。如果你有N数据点在D您想要映射到的尺寸Y尺寸,然后
t-SNE是有序的D*N2操作。
Barnes-Hut t-SNE开始有序运作D*N日志(N) * exp(维度(Y))操作。
对于大的数据集N大于1000左右,嵌入维数在哪里Y是2或3,Barnes-Hut算法可以比精确算法更快。
有用的非线性失真
T-SNE将高维距离映射到扭曲的低维类似物。因为那个学生的尾巴比较肥t低维空间的分布,tsne通常将近距离移动近距离移动,并且远远超过比高维空间更远的点,如下图所示。该图显示了高斯和学生t在密度为0.25和0.025点处的分布。高斯密度与高维距离有关t密度与低维距离有关。的t与高斯密度相比,密度对应于闭点更近,远点更远。
t = linspace (0 5);日元= normpdf (t, 0,1);y2 = tpdf (t, 1);情节(t, y1,“k”,t,y2,“r”) 抓住在x1 = fzero (@ (x) normpdf (x, 0,1) -0.25, (0, 2));x2 = fzero (@ (x) tpdf (x, 1) -0.25 (0, 2));z1 = fzero (@ (x) normpdf (x, 0,1) -0.025, [0, 5]);z2 = fzero (@ (x) tpdf (x, 1) -0.025, [0, 5]);情节([0 x1], [0.25, 0.25],“k -”。)图([0,Z2],[0.025,0.025],“k -”。)图([x1,x1],[0,0.25],'G-',[x2,x2],[0,0.25],'G-')图((z1, z1), [0, 0.025],'G-', (z2, z2], [0, 0.025],'G-')文本(1.1,二十五分,Close point在low-D中更接近)文本(2.4、0。'远的点在低D'中更远) 传奇('高斯(0,1)','学生t(df = 1)')xlabel(“x”)ylabel('密度')标题('高斯分布密度(0,1)和学生t (df = 1)') 抓住离开
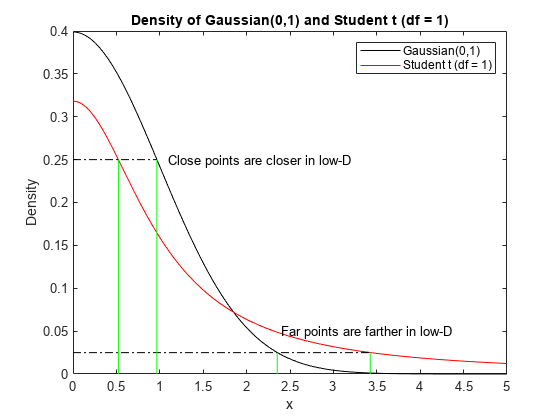
这种扭曲在应用时是有帮助的。它并不适用于高斯方差高的情况,高斯方差高会降低高斯峰,使分布变平。在这种情况下,tsne可以比原始空间相距远更远的近距点。为了达到乐于助人的扭曲,
设定
“详细”名称-值对2.调整
“困惑”名称-值对,因此报告的方差范围不会太远1,均值方差接近1.
如果可以达到这一范围的差异,那么图表适用,而且tsne失真是有益的。
有效曲调的方法tsne参见Wattenberg, Viégas和Johnson[4].
参考文献
[1] van der Maaten, laurence和Geoffrey Hinton。“可视化数据使用t-Sne。“J.机器学习研究9, 2008, pp. 2579-2605。
[2]范德马顿,劳伦斯。Barnes-Hut-SNE.arxiv:1301.3342 [cs.lg], 2013年。
罗伯特·雅各布斯“通过学习速率的适应来提高收敛速度。”神经网络1.4,1988,第295-307页。
[4] Wattenberg, Martin, Fernanda Viégas,和Ian Johnson。《如何有效使用t-SNE》。蒸馏,2016.可用如何有效使用t-SNE.

