菲德勒的同伴矩阵分配一个多项式的系数沿对角线的一个优雅的对角矩阵的特征值都等于0的多项式。gydF4y2Ba

内容gydF4y2Ba

Miroslav菲德勒gydF4y2Ba

我几周前在伯克利度过了非常愉快的一天和我的朋友贝雷斯福德Parlett。访问期间他告诉我一个优雅的版本的相关矩阵Miroslav菲德勒2003年推出。菲德勒捷克数学家出名的是他的贡献,线性代数、图论和两者之间的联系。他经常参加家长座谈会,在不同时期,组织委员会的成员。gydF4y2Ba

传统的同伴矩阵gydF4y2Ba

MATLAB通常代表一个多项式的学位n美元与n + 1美元组件一个向量。这样一个代表,主要的词有自己的系数,这可能是零。在这篇文章中,我想要gydF4y2Ba首一gydF4y2Ba领先多项式,系数是1,所以只有n美元组件对应的向量。gydF4y2Ba

$ $ p (x) = x ^ n + a_1 x ^ {n} + a₂^ {2} +……+现代x + an $ $ {n}gydF4y2Ba

每个这样的多项式gydF4y2Ba同伴矩阵gydF4y2Ba而系数沿第一行,沿着第一副斜杆的。这种传统的同伴矩阵是由光滑的MATLAB代码生成。gydF4y2Ba

类型gydF4y2Ba同伴gydF4y2Ba

函数C =同伴(一)n =长度(一个);C = [——;眼睛(n, n));gydF4y2Ba

这是传统的同伴系数矩阵gydF4y2Ba1:10gydF4y2Ba。gydF4y2Ba

同伴(1:10)gydF4y2Ba

ans = 1 2 3 4 5 6 7 8 9 -10 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0gydF4y2Ba

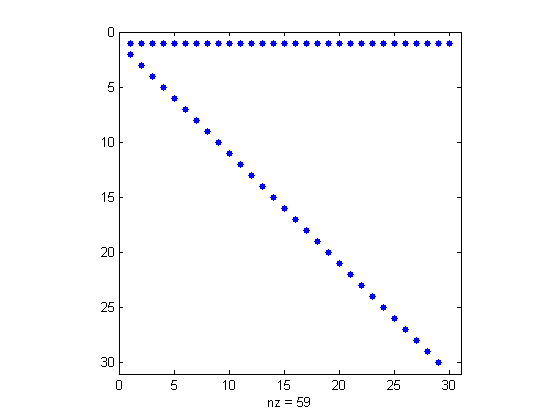
这是gydF4y2Ba间谍gydF4y2Ba图30系数。gydF4y2Ba

间谍(同伴(1:30))gydF4y2Ba

菲德勒同伴矩阵gydF4y2Ba

菲德勒显示我们可以生成一个不同的伴侣安排系数矩阵,与零交流,一起沿着超级副斜杆,沿着supersuper 1和0,subsubdiagonal对角矩阵。我爱的MATLAB代码生成菲德勒同伴矩阵。gydF4y2Ba

类型gydF4y2Ba菲德勒gydF4y2Ba

函数F =菲德勒(a) n =长度(一个);b =的(n - 1);b (1:2: n - 2) = 0;c =——(2: n);c (1:2: n - 1) = 0;c (1) = 1;d =——(2: n);d (2:2: n - 1) = 0;e =的(n - 1);e (2:2: n - 2) = 0; F = diag(b,-2) + diag(c,-1) + diag(d,1) + diag(e,2); F(1,1) = -a(1);

这是菲德勒同伴系数矩阵gydF4y2Ba1:10gydF4y2Ba。gydF4y2Ba

菲德勒(1:10)gydF4y2Ba

ans = 1 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 4 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 5 0 6 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 7 0 8 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 9 0 -10 0 0 0 0 0 0 0 1 0 0gydF4y2Ba

这是gydF4y2Ba间谍gydF4y2Ba图30系数。gydF4y2Ba

间谍(菲德勒(1:30))gydF4y2Ba

根gydF4y2Ba

当我写第一个Fortran MATLAB在1970年代末,我包含了gydF4y2Ba根gydF4y2Ba函数。我承认现在几乎是超过一个快速攻击。gydF4y2Ba根gydF4y2Ba找到一个多项式的零点设置(繁体)同伴矩阵和调用gydF4y2BaeiggydF4y2Ba函数来计算其特征值。我包含这个函数有两个原因。首先,它给了我一个多项式零点仪以非常小的成本的额外代码。第二,它将寻找矩阵特征值的线性代数教材的方法计算特征多项式的0。但我不确定gydF4y2Ba根gydF4y2Ba总是准确的。gydF4y2Ba

我是幸运的。gydF4y2Ba根gydF4y2Ba原来是一个好主意。15年后发表的论文Kim-Chuan(音)和尼克•Trefethen和艾伦•埃德尔曼和h村上成立,只要gydF4y2Ba平衡gydF4y2Ba使用,gydF4y2Ba根gydF4y2Ba数值可靠。gydF4y2Ba

另一方面,gydF4y2Ba根gydF4y2Ba可以从效率的角度批评。O (n)美元一个多项式系数。我不知道零发现问题的计算复杂性,但复杂的矩阵特征值问题是O (n ^ 2)存储和美元O (n ^ 3)美元,这的确是太多了。gydF4y2Ba

这是菲德勒进来的地方。菲德勒可以取代传统的同伴矩阵gydF4y2Ba根gydF4y2Ba。现在,如果我们能找到一个矩阵特征值的算法,适用于非对称五对角矩阵在O (n)存储和美元O (n ^ 2)美元,然后我们会最终gydF4y2Ba根gydF4y2Ba。gydF4y2Ba

威尔金森10gydF4y2Ba

例如,让我们使用gydF4y2Ba威尔金森多项式gydF4y2Ba与根1到10。gydF4y2Ba

信谊gydF4y2BaxgydF4y2Bap = prod (x - (1:10)) p =扩大(p) =多项式系数(p);F =菲德勒(双(fliplr ((1: end-1))))gydF4y2Ba

p = (x - 1) * (x - 2) * (x - 3) * (x - 4) * (x - 5) * (x - 6) * (x - 7) * (x - 8) * (x - 9) * (x - 10) p = x ^ 10 - 55 * x ^ 9 + 1320 * x x ^ ^ 8 - 18150 * 7 + 157773 * x ^ 6 - 902055 * x ^ 5 + 3416930 * x ^ 4 - 3416930 * x ^ 3 + 12753576 * x ^ 2 - 10628640 * x + 10628640 F = 1到6列55 -1320 1 0 0 0 0 0 0 0 0 0 18150 -157773 0 1 0 0 1 0 0 0 0 0 0 0 902055 0 -3416930 0 0 0 1 0 0 0 0 0 0 0 8409500 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0列7到10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 -12753576 1 0 0 0 0 0 0 10628640 0 10628640 0 1 0 0gydF4y2Ba

看看这些系数。你能想象什么弯曲一个向量v必须经过美元为了满足阵线= \λv $美元整数\λ1到10美元吗?结果,计算特征值F显示美元的精确度损失所致gydF4y2Ba的敏感性gydF4y2Ba这个多项式的根。gydF4y2Ba

格式gydF4y2Ba长gydF4y2Baλ= eig (F)gydF4y2Ba

λ= 9.999999999992546 8.999999999933312 8.000000000317854 6.999999999479941 6.000000000423509 4.999999999814492 4.000000000042952 2.999999999995175 2.000000000000225 0.999999999999996gydF4y2Ba

平衡gydF4y2Ba

对称矩阵有良好条件特征值。平衡、Parlett Reinsch,引入的一个想法是试图找到一个使一个非对称矩阵的对角相似变换“更近对称”,在这个意义上的规范行和列的标准接近相等。平衡并不总是可能的。例如,一个上或下三角矩阵不能平衡。三角矩阵非对称的不可救药,但没关系,因为他们的特征值都是对角线上。gydF4y2Ba

默认情况下,MATLAB,使用LAPACK,平衡非对称矩阵在计算特征值。(和Trefethen,埃德尔曼和村上,强调,这对数值的稳定性至关重要gydF4y2Ba根gydF4y2Ba。也是同样的道理gydF4y2Ba根gydF4y2Ba根据菲德勒矩阵。当我们叫gydF4y2BaeiggydF4y2Ba以上,MATLAB平衡输入矩阵。它帮助很多。gydF4y2Ba

平衡是通过两个孩子的权力,这样就不会引入任何舍入错误。大元素是按比例缩小明显,而在外斜线扩大的只有少数的两种能力。这是平衡菲德勒矩阵。gydF4y2Ba

格式gydF4y2Ba短gydF4y2BaB =平衡(F)gydF4y2Ba

B = 1到7列55.0000 -20.6250 32.0000 64.0000 0 0 0 0 0 0 0 0 0 0 0 0 8.8623 16.0000 -4.8148 - 8.0000 0 0 0 0 0 0 0 0 0 0 0 0 -3.2586 4.0000 3.4411 0 0 0 0 0 0 0 0 0 0 0 2.0050 4.0000 2.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0列8到10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1.5203 - 2.0000 0 0 0 0 0 -0.4326 0.5000 0.6335 0 0gydF4y2Ba

平衡降低矩阵的标准由五个数量级。这是之前和之后。gydF4y2Ba

格式gydF4y2Ba短gydF4y2BaggydF4y2Badisp (gydF4y2Ba“不平衡的平衡”gydF4y2Ba)disp((规范(F)规范(B)))gydF4y2Ba

不平衡的平衡1.8092 e + 07年88.433gydF4y2Ba

有时,但不是经常,需要绕过平衡。这是当矩阵包含小元素,是舍入的结果或其他错误,不应该扩大成为类似的其他元素。没有任何这样的元素在这个矩阵。gydF4y2Ba

这是计算特征值,没有和平衡。gydF4y2Ba

格式gydF4y2Ba长gydF4y2Badisp (gydF4y2Ba“不平衡的平衡”gydF4y2Ba)disp (eig (F,gydF4y2Ba“nobalance”gydF4y2Ba)eig (F))gydF4y2Ba

不平衡的平衡9.999999330734642 9.999999999992546 8.999996381627081 8.999999999933312 8.000028620785038 8.000000000317854 6.999932559108236 6.999999999479941 6.000079411601993 6.000000000423509 4.999948356986658 4.999999999814492 4.000018256147182 4.000000000042952 2.999996926380218 2.999999999995175 2.000000155398907 2.000000000000225 1.000000001522463 0.999999999999996gydF4y2Ba

你必须看到后面的数字特征值计算不平衡不太准确。很明显,当我们计算错误。平衡的五个数量级提高精度是通过减少输入的标准。gydF4y2Ba

格式gydF4y2Ba短gydF4y2BaegydF4y2Badisp (gydF4y2Ba平衡不平衡的gydF4y2Ba)disp ((eig (F) - (10: 1:1) ' eig (F,gydF4y2Ba“nobalance”gydF4y2Ba)- (10:1:1)'])gydF4y2Ba

平衡不平衡-7.4536 2.8621 3.1785 -3.6184 -6.6688 -6.6927 e-12 e-07 e-11 e-06平台以及e-05 -5.2006平台以及-6.7441 e-05 4.2351平台以及7.9412 e-05 -1.8551平台以及-5.1643 2.2515 -3.0736 -4.8255 1.8256 4.2952 e-05 e-11 e-05 e-12 e-06 e-13 e-09 1.5225 -3.7748 1.5540 e-07 e15汽油gydF4y2Ba

相似运动gydF4y2Ba

传统的同伴矩阵和菲德勒同伴矩阵是相似的。你能找到的相似变换吗?它有一个非常有趣的非零结构。gydF4y2Ba

结论gydF4y2Ba

如果我们能找出如何利用对角结构,Miraslav菲德勒优雅的同伴矩阵将是一个全能冠军,但我们决不能忘记平衡。gydF4y2Ba

引用gydF4y2Ba

Miroslav菲德勒,注意同伴矩阵,线性代数及其应用372 (2003),325 - 331。gydF4y2Ba

艾伦•埃德尔曼和h村上多项式根的同伴矩阵特征值,数学计算。64 (1995),763 - 776,gydF4y2Ba< http://www-math.mit.edu/ edelman /网页/论文/ companion.pdfgydF4y2Ba>gydF4y2Ba

Kim-Chuan(音)和劳埃德n . Trefethen Pseudozeros多项式和pseudospectra同伴矩阵,号码。数学。68:(1994)403 - 425,gydF4y2Ba< http://people.maths.ox.ac.uk/ trefethen _61.pdf /出版/ PDF / 1994gydF4y2Ba>gydF4y2Ba

克里夫硅藻土,克里夫的角落:根——多项式的,也就是说,gydF4y2Ba< //www.tatmou.com/company/newsletters/articles/roots-of-polynomials-that-is.htmlgydF4y2Ba>gydF4y2Ba

贝雷斯福德Parlett和基督教Reinsch平衡矩阵特征值和特征向量的计算,号码。数学。,13,(1969), 293-304,< http://link.springer.com/article/10.1007/BF02165404gydF4y2Ba>gydF4y2Ba

得到了MATLAB代码gydF4y2Ba

发表与MATLAB®R2014agydF4y2Ba

发表与MATLAB®R2014agydF4y2Ba