在回顾了50年前的情况后，我使用经典的有限差分方法，然后进行外推，找到MathWorks标识下区域的第一个特征值。

内容

五十年前

1965年，我向斯坦福数学系提交了博士论文，题目是“拉普拉斯算子特征值的有限差分方法”。这篇论文不仅仅是关于L型区域的，L是我的主要例子。

我的论文导师是乔治·福赛斯(George Forsythe)，他在自己的一些研究中研究了L。当时，许多人对获得微分算子特征值的保证上界和下界的方法感兴趣。Forsythe已经证明了某些有限差分方法可以为凸区域提供下界。但是L不是凸的，所以这是一个需要研究的区域。

没人确切地知道第一个特征值。Forsythe和Wolfgang Wasow在1960年出版了一本书，“偏微分方程的有限差分方法”(John Wiley & Sons)，在几个不同的部分都有L的特征。在第24.3节中，Forsythe引用了他在1954年所做的一些计算，这些计算使他做出了这一估计

$$ \lambda_1 = 9.636 $$

他接着报告了他的同事R. De Vogelaere在50年代末提出的一个非正式猜想

< \lambda_1 < 9.63972 $$

我在这里重复这些数字是为了让你们了解我们当时的工作精度。我们将在后面的文章中看到，正确答案就在德·沃吉拉尔的上界之外。

我在1964年的计算

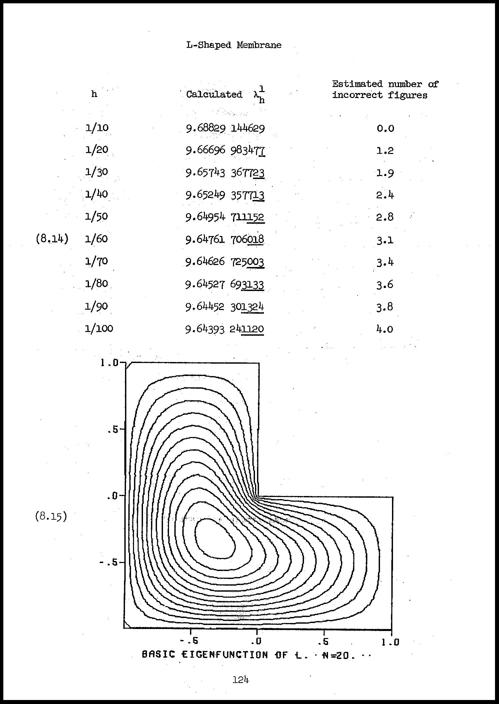
这是我论文的一页。页面底部的等高线图最终会演变成MathWorks标志。情节是在一个数控绘图机绘图机这是一种由计算机控制的螺线管，手持圆珠笔或液体墨水笔，在旋转滚筒上滚动的纸张上移动。这是一种非常有效的设备，在世界各地的计算机中心使用了很多年。

本页上显示的计算是10个网格大小为$h$的拉普拉斯有限差分的第一个特征值。最细的网格，$h$ = 1/100，有29601个内部点。我记得，第一个特征值的计算，我用了一种逆幂法，在斯坦福大学的主机上花了大约半个小时，那是一台IBM 7090。

这是我50年前计算的这些数值的图表。我加了一条黑线在我们现在知道的极限值处，连续微分算子的第一个特征值。你可以看到有限差分值收敛得很慢。此外，它们正从上方汇聚。Forsythe不会得到这个非凸区域的下界。

thesis_graph

收敛速度慢

有限差分特征值的收敛速度随网格尺寸的减小是由于对应的特征函数在该区域的可重入角处是奇异的。在这个角处梯度变为无穷大。你可以看到轮廓线在角落附近挤在一起。如果你试图在l型框架上拉伸一层膜来制作鼓头或手鼓，它会撕裂。

更精确地说，使用极坐标$r$和$\theta$，以可重入角为中心。注意，为了覆盖区域的内部，$\theta$将从$0$到$\frac{3}{2}\pi$。结果表明，在趋近角时第一个本征函数具有渐近特性

$$ u(r，\theta) \约r^\alpha \sin{\alpha \theta} $$

与$\alpha = \frac{2}{3}$。这意味着本征函数的k阶导数具有类似的奇点

$$ \partial^k u \ approximately r^{\alpha-k} $$

将这一事实与五点有限差分算子离散误差的泰勒级数分析相结合，我们发现第一个特征值以速率收敛

$ $ \ lambda_ {1 h} - \ lambda_1 \大约O (h ^{2 \α})= O (h ^ \压裂{4}{3})$ $

这明显比当本征函数非奇异时得到的$O(h^2)$收敛速度慢。

MATLAB中的差分法

现在让我们使用我的笔记本电脑和MATLAB中的稀疏功能。的函数numgrid，delsq，间谍,eigs都被列入了sparfun目录自引入以来。我们首先生成一个小的l型编号方案。

N = 10;L = numgrid(“L”n + 1)

L = 0 0 0 0 0 0 0 0 0 0 0 0 1 5 9 13 17 21 30 39 48 14 0 0 2 6 10 18 22日31日40 49 0 0 3 7 11 15 19 23 32 41 50 0 0 4 8 12 16 20 24 33 51 42 0 0 0 0 0 0 0 25 34 43 52 0 0 0 0 0 0 0 26 35 44 53 0 0 0 0 0 0 0 27 36 45 54 0 0 0 0 0 0 0 28 37 46 55 0 0 0 0 0 0 0 29 38 47 56 0 0 0 0 0 0 0 0 0 0 0 0

为了说明该方案是如何工作的，将其叠加在有限差分网格上。

Lgrid(左)

该声明

A = delsq(L);

构造了网格五点离散拉普拉斯矩阵的矩阵表示l．

谁一个issym = isequal(A,A') nnzA = nnz(A)

名称大小字节类属性A 56x56 3156 double sparse issym = 1 nnzA = 244

对于这个网格，离散拉普拉斯矩阵一个是一个具有244个非零元素的56 × 56稀疏双精度对称矩阵。这是一个平均值

ratio = nnz(A)/size(A,1)

比率= 4.3571

每行非零元素。每个内部网格点都与四个最近的邻居相连。例如，44号点与35、43、45和53号点相连。第44列中的非零元素是

(: 44)

ans =(35岁,1)1(43岁,1)1(44岁,1)4(45岁,1)1(53岁,1)1

对角线上有4，而-1是对角线外的位置，对应于相邻的连接。它们可以在间谍显示非零的位置的图形。

间谍(A)

规模一个按网孔大小的平方再用eigs求它的五个最小特征值。

h = 2/n A = A/h²;eigvals = eigs(A,5，“sm”）

H = 0.2000 eigvals = 30.3140 27.7177 19.0983 14.6708 9.6786

2014年我的计算

运行减少网格大小，直到我的笔记本电脑的内存容量。

类型L_finite_diffs

MathWorks Logo的脚本，第二部分%有限差分选项。Tol = 1.0e-12;Eigvals = 0 (13,5);L = numgrid('L'，n+1);H = 2/n;A = delsq(L)/h^2;e = eigs(A,5，'sm'，opts);Eigvals (n/50，:) = fliplr(e');流(4.0 ' % % 10.6 f % 9.0 f % 10.0 f % 16.12 f \ n ',…n,h,size(A,1)，nnz(A)，e(5)) end toc save eigvals

类型L_finite_diffs_results

n h size(A) nnz(A) lambda_1,h 50 0.040000 1776 8684 9.661331286788 100 0.020000 7301 36109 9.649547111146 150 0.013333 16576 82284 0.010000 29601 147209 9.64393232382 250 0.008000 46376 230884 9.642903412412 300 0.005714 91176 454484 9.641797238078 400 0.005000 119201 594409 9.641471331746 450 0.004444 150976 753084 9641225852818 500 0.004000 186501 930509 500 0.003636 225776 1126684 9.640883203502 600 0.003333 2688011341609 9.640759699387 650 0.003077 315576 1575284 9.640657572983运行时间为29.729023秒。

外推法

我知道离散化误差的泰勒级数分析涉及$h^{4/3}$和$h^2$，所以让我们使用这些作为外推的基础。使用反斜杠做最小二乘拟合。

负载eigvalsEigvals = Eigvals (:，1);N = (50:50:650)';H = 2./n;E = ones(size(h));X = [e h.^(4/3) h.^2];c = X(4:end，:)\eigvals(4:end);Lambda1 = c(1);N = (50:10:650)';H = 2./n;拟合= c(1) + c(2)*h.^(4/3) + c(3)*h.^2; plot(n(1:5:end),eigvals,“o”n,健康,“- - -”，[0 700]，[lambda1 lambda1]，“k -”甘氨胆酸)组(,“xtick”100:100:600,“xticklabel”，.．.num2str (sprintf (“2 / % 3.0 f \ n”, 100:100:600)))包含(“h”）

坦白地说，当有限差分特征值的外推产生这个结果时，我很惊讶。

格式长λ₁

Lambda1 = 9.639723753239963

从我将在以后的文章中描述的技术中我知道这与连续微分算子的精确特征值一致，直到小数点后7位。在我写这篇博客之前，我从来没有在有足够内存来处理网格的计算机上尝试过这种计算，也从来没有能够从外推的有限差分特征值中获得这种精度。

本征函数

我们画一个特征函数的等高线图。棘手的部分是使用网格编号l把特征向量插入到网格上。

Close n = 100;H = 2/n;L = numgrid(“L”n + 1);A = delsq(L)/h^2;[V,E] = eigs(A,5，“sm”）;L(L>0) = -v (:，5);contourf (fliplr (L)、12);轴广场轴从

情节显示parula， MATLAB默认配色图Handle Graphics II和Release 2014b。颜色映射的名称来源于parula这是一种遍布北美东部的小型莺，呈现出这些颜色。正如我们的等高线图所示，随着等高线水平的增加，颜色强度平滑均匀地变化。这不是真的飞机，旧的默认值。史蒂夫·埃丁有更多关于parula在他的博客里。

获取MATLAB代码

发布与MATLAB®R2014b