当牛顿法的出发点不是函数的接近零,全球行为似乎是不可预测的。等高线的迭代计算收敛区域的起始点复平面生成发人深省的分形图像。我们的示例使用最近的两个帖子的主题,历史立方$ x ^ 3-2x-5美元。

内容

历史性的立方

今天所有的图像产生的立方$ x ^ 3-2x-5美元前两个帖子的主题,a-historic-cubic和testing-zero-finders。$ $ F (z) = z ^ 3-2z-5 $ $

F = @ (z) z。^ 3 - 2 * z-5;

牛顿法还需要导数。$ $ F ' (z) = 3 z ^ 2 - 2 $ $

Fprime = @ (z) 3 * z。^ 2 - 2;

牛顿迭代器

这是进行牛顿迭代的功能,在指定的点开始在复平面。函数返回结果的零和计算所需的迭代次数达到它。这些数量是分形图像的基础。

类型牛顿

函数[z, kount] =牛顿牛顿(F, Fprime, z) %。[z, kount] =牛顿(F, Fprime, z)。%开始为函数F牛顿法和导数Fprime %标量复杂点z。返回聚合值迭代kount z和%。sqrteps =√eps (2);kount = 0;w =正;而abs (z-w) > sqrteps kount = kount + 1;w = z;z - z = F (z)。/ Fprime (z);结束结束

分形的观点

这个函数使用contourf生产两个彩色的轮廓图。第一个显示了一个正方形网格迭代计算的起点。第二个是基于极坐标角度计算的零。只有三个轮廓水平在第二个情节,对应的三个零立方。

类型分形

分形函数(F Fprime z0 d n);%分形。分形(F, Fprime z0 d n)。%调查牛顿法生成的分形图像%与导数函数F (z) Fprime (z) %开始(n + 1)——- (n + 1)复杂电网集中在%与半角点z0 d . x =实际(z0) + (1:2 / n: 1) * d;y =图像放大(z0) + (1:2 / n: 1) * d;[y、x] = ndgrid (x, y);z = x + i * y;kounts = 0(大小(z));k = 1:长度(z (:)) [z (k), kounts (k)] =牛顿(F Fprime z (k));图(1)水平= min (kounts (:)) + (0:10); contourf(xs,ys,kounts,levels) colorbar axis square figure(2) zone = round(atan2(imag(z),real(z))/pi); contourf(xs,ys,zone,-1:1) colorbar('Ticks',(2/3)*(-1:1),'Ticklabels',{'-2\pi/3',0,'2*\pi/3'}) c = [1 1 0; 0 1 1; 1 0 1]; colormap(c) axis square end

鸟瞰

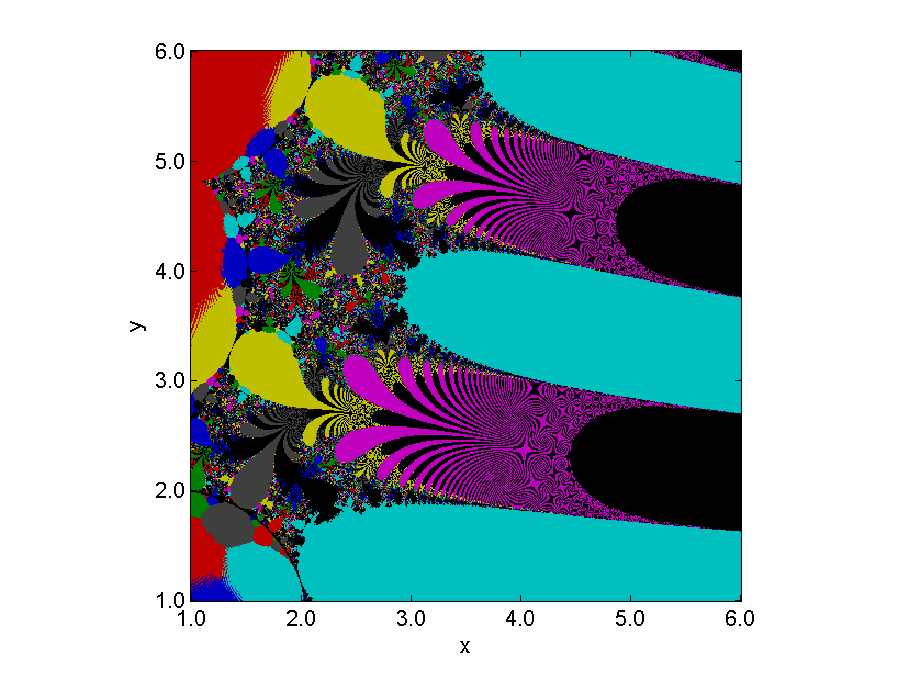
我们最大的地区集中在最初的30,半角。复平面分为三分之二是由射线来自原点沿负实轴和极角美元\ \下午压裂{\π}{3}$。附近所有的分形行为发生其中一个分隔符。迭代不启动分离器附近收敛于零的开始。轮廓充满了橙色和黄色和相关colorbar告诉我们,大多数迭代开始离原点的距离大于30至少需要12个步骤收敛。

分形(F Fprime 0, 30512)

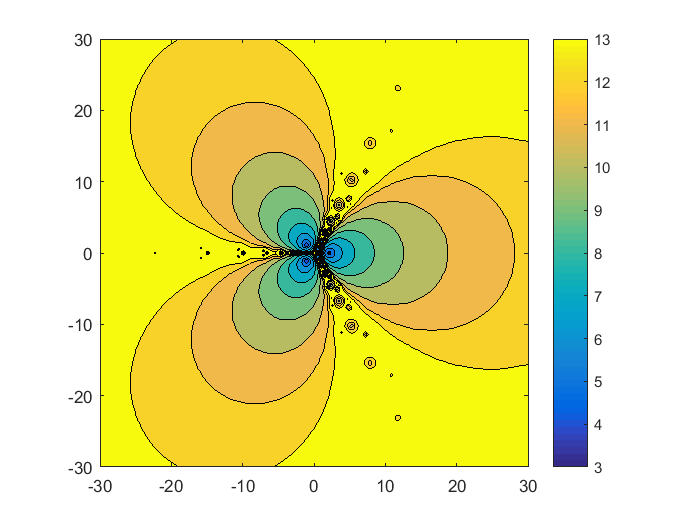
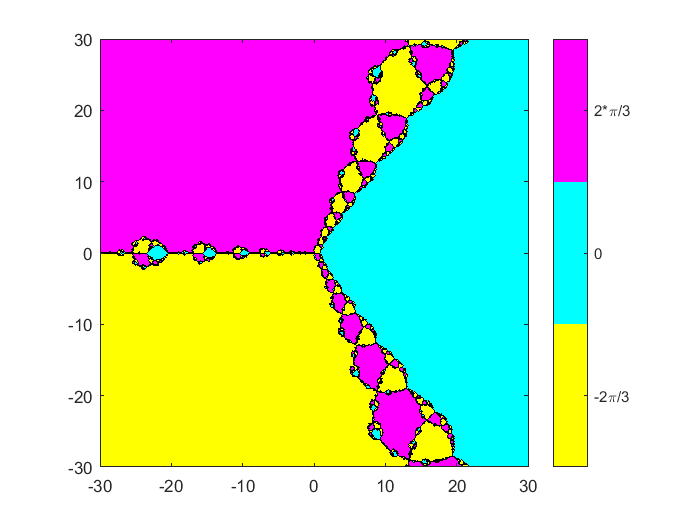
放大的起源

放大10倍。现在半角3。函数计算的三个蓝色轮廓水平最低的围绕着三个零。这就是牛顿法适用;开始接近零和迭代收敛几步到零。区域分离三个最小值有较高的迭代计算和更复杂的行为。导数$ F (x) = 3 x ^ 2 = 0美元$ $ x = \ \下午√6{\压裂{2}{3}}\大约\ pm 0.816 $ $ $ F '的牛顿迭代器(x)美元在分母波兰人在这两点。二阶导数F (x) = 6 x美元是零在原点。轮廓图显示四分支模式在原点和阳极三分支模式。这两个模式反复出现在所有尺度分形。

分形(F Fprime 0, 3512)

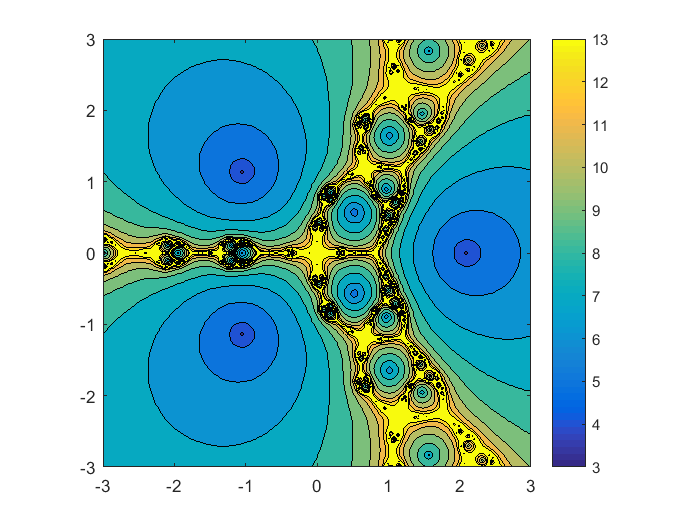
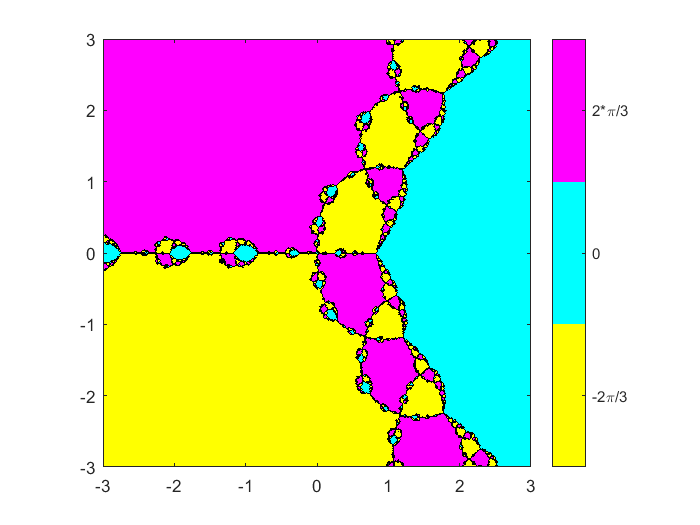
细节在原点。

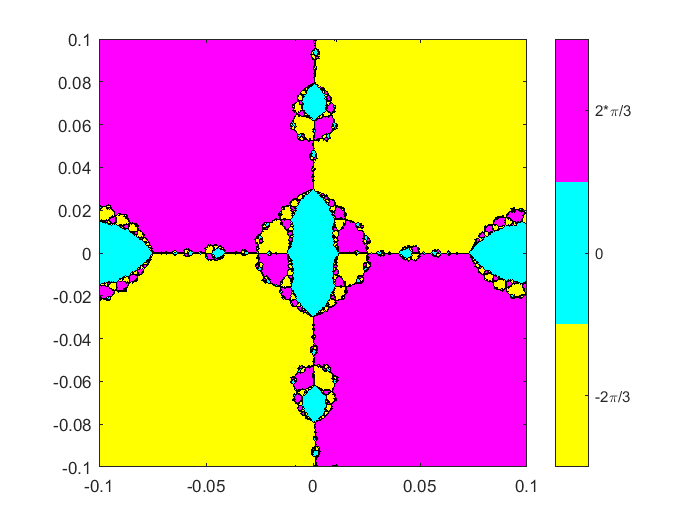
放大30的另一个因素。如今,半宽度是0.1。我们可以看到详细四分支模式。第二本地区等高线图大部分是彩色的红色或黄色,表明大多数迭代收敛于一个复杂的零在左半平面。一个相对较小的部分是彩色的青色,表明收敛到正实轴上的零不太频繁。

分形(F, Fprime 0 0.1,512)

在一个极

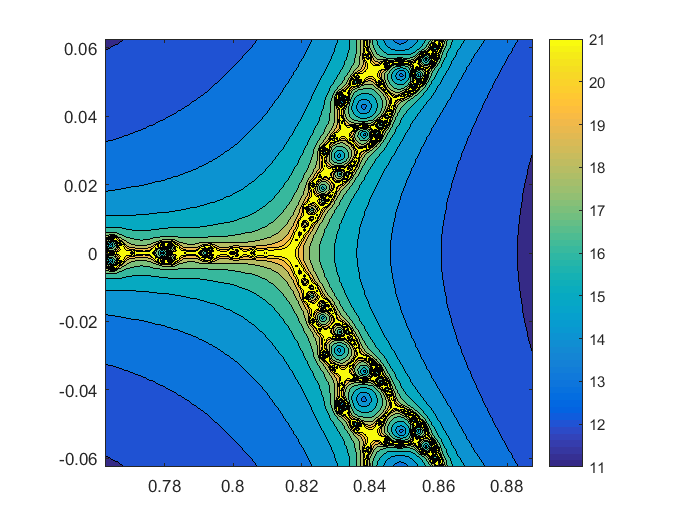
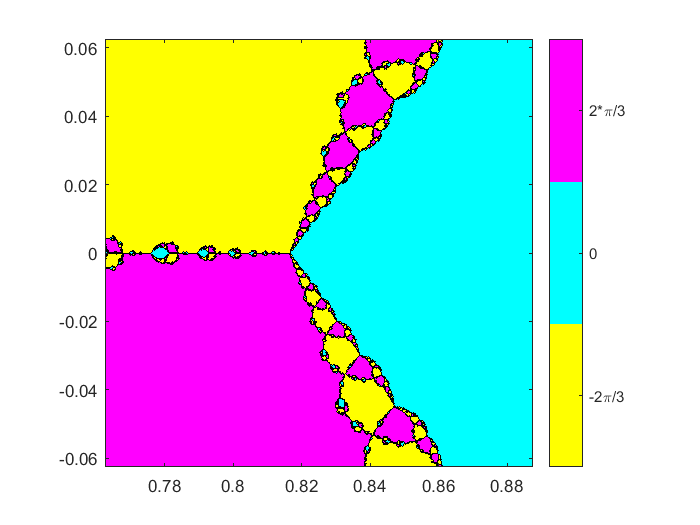
锅的钢管$ x = .816 $。我们看到一个三方分离器与同一地区的三种颜色,红色、黄色和青色。迭代开始附近这杆也同样可能收敛于每个三个零。

分形(F Fprime .825 1/16,512);

放大10 ^ 6,colormap翻转

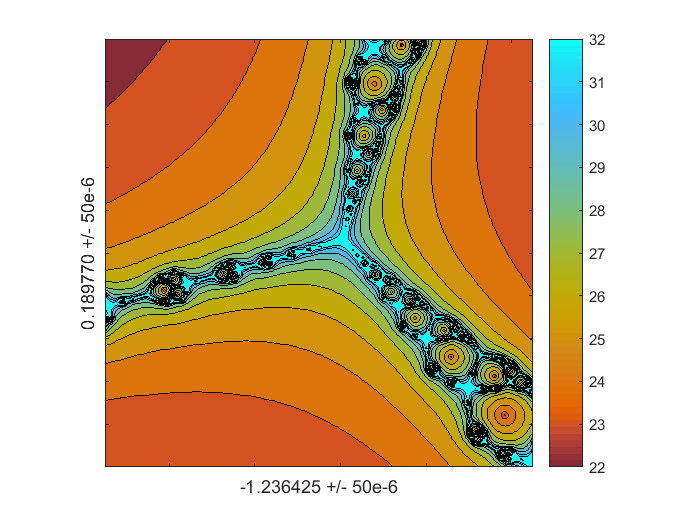
放大了近六个数量级在复平面上一个点略高于负实轴。我们看到一个稍微旋转三分支模式的重复。玩很有趣的颜色通过互换角色默认colormap,红色和蓝色的parula。

z0 = -1.236425 + 0.189770我;d = 50 e-6;图(1)colormap (fliplr (colormap));分形(F, Fprime z0 d, 512)标签(“-1.236425”,“0.189770”,“50 e-6”)

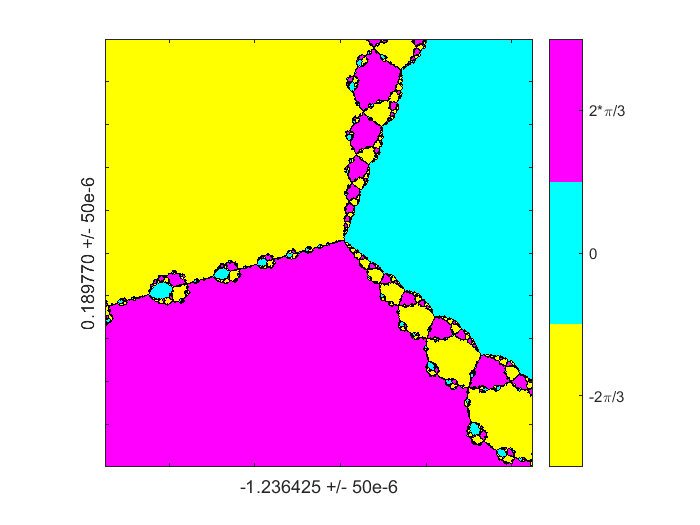
放大10 ^ 8

放大了近8个数量级的分离器在正确的半平面上的一点。我们现在都三路和四路模式,尽管他们有不同的颜色,因为我翻colormap。

z0 = 0.73244050 + 1.73490150我;d = 25 e-8;分形(F, Fprime z0 d, 512)标签(“0.73244050”,“l.73490150”,“25 e-8”)

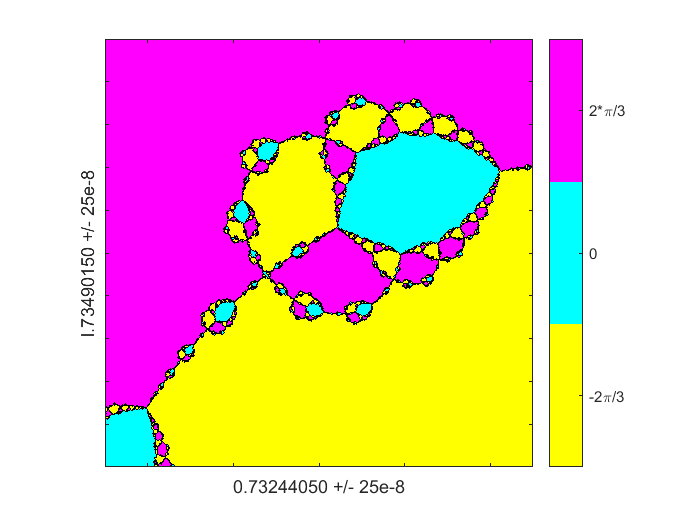
多一个

这是我的最后一个。注意,迭代计数增加了至少25。尽管牛顿法收敛需要更长的时间,我们仍然看到相同的三、四分支行为模式。

z0 = 0.73244062 + 1.73490165我;d = 4 e-8;图(1)colormap(铜);分形(F, Fprime z0 d, 512)标签(“0.73244062”,“l.73490165”,“4 e-8”)

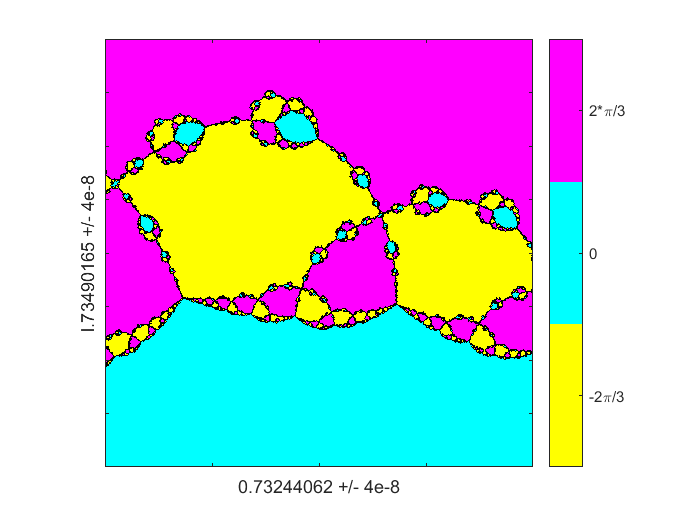
引用

全球行为的分形性质的牛顿法是众所周知的。如果你问谷歌“牛顿分形”,你会得到许多有趣的链接。查看图片和电影。如果你问“MATLAB牛顿分形”,你会得到一些有趣的链接,包括MATLAB中央的贡献。我非常喜欢分形。我已经写过曼德布洛特集在与MATLAB实验。我也写了一个博客两年前的分形生成的循环塔的力量函数z ^ $ $ {z ^ {z ^ z}} $ $

得到了MATLAB代码发表与MATLAB®R2015a