当牛顿方法的起点未接近函数的零时，全局行为似乎是不可预测的。迭代的轮廓曲线绘制到复杂平面中的起始点区域的收敛，从而产生思想挑衅分形图像。我们的例子采用了最近帖子的主题，历史悠久的立方标记x ^ 3-2x-5 $。

内容

历史性的立方

今天所有的图像都是由立方$x^3-2x-5$生成的，这是前两篇文章的主题，a-historic-cubic和测试零点．$$ f（z）= z ^ 3-2z-5 $$

f = @（z）z。^ 3-2 * z-5;

牛顿法也需要导数。$ F'(z) = 3z^2-2 $

f ' = @(z) 3*z.^2;

牛顿迭代器

这是执行牛顿迭代的函数，从复平面上的一个指定点开始。该函数返回结果0和达到该值所需的迭代次数的计数。这些计数是分形图像的基础。

类型牛顿

功能[z，kount] = newton（f，fprime，z）％牛顿。[z，kount] =牛顿（f，fprime，z）。％在标量复数z处启动牛顿功能f的方法和衍生fprime％。返回融合值z和％迭代kount。sqrteps = sqrt（eps（2））;kount = 0;w = inf;虽然abs（z-w）> sqrteps kount = kount + 1;w = z;z = z  -  f（z）./ fprime（z）; end end

分形的观点

此功能使用contourf.绘制两幅彩色等高线图。第一个显示了起点的正方形网格的迭代计数。第二种是基于计算出的零点的极角。在第二幅图中只有三个等高线，对应于立方体的三个零。

类型分形

分形函数(F Fprime z0 d n);%分形。分形(F, Fprime z0 d n)。研究由牛顿方法生成的分形图像，其中函数F(z)的导数为Fprime(z) %，开始于(n+1)-by-(n+1)复合网格，以% the point z0 with half-width d为中心。y =图像放大(z0) + (1:2 / n: 1) * d;[y、x] = ndgrid (x, y);z = x + i * y;kounts = 0(大小(z));k = 1:长度(z (:)) [z (k), kounts (k)] =牛顿(F Fprime z (k));End figure(1) levels = min(count (:)) + [0:10]; contourf(xs,ys,kounts,levels) colorbar axis square figure(2) zone = round(atan2(imag(z),real(z))/pi); contourf(xs,ys,zone,-1:1) colorbar('Ticks',(2/3)*(-1:1),'Ticklabels',{'-2\pi/3',0,'2*\pi/3'}) c = [1 1 0; 0 1 1; 1 0 1]; colormap(c) axis square end

鸟瞰

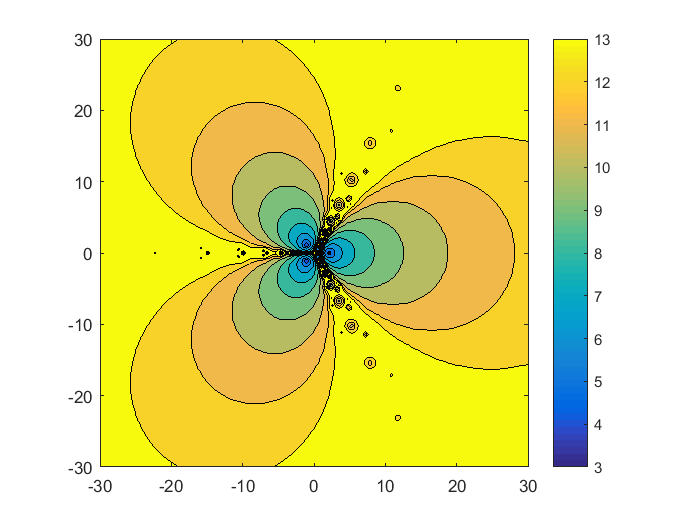
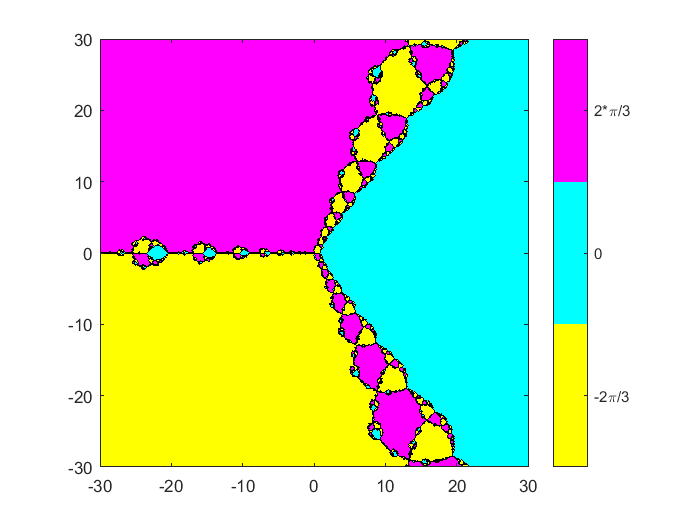
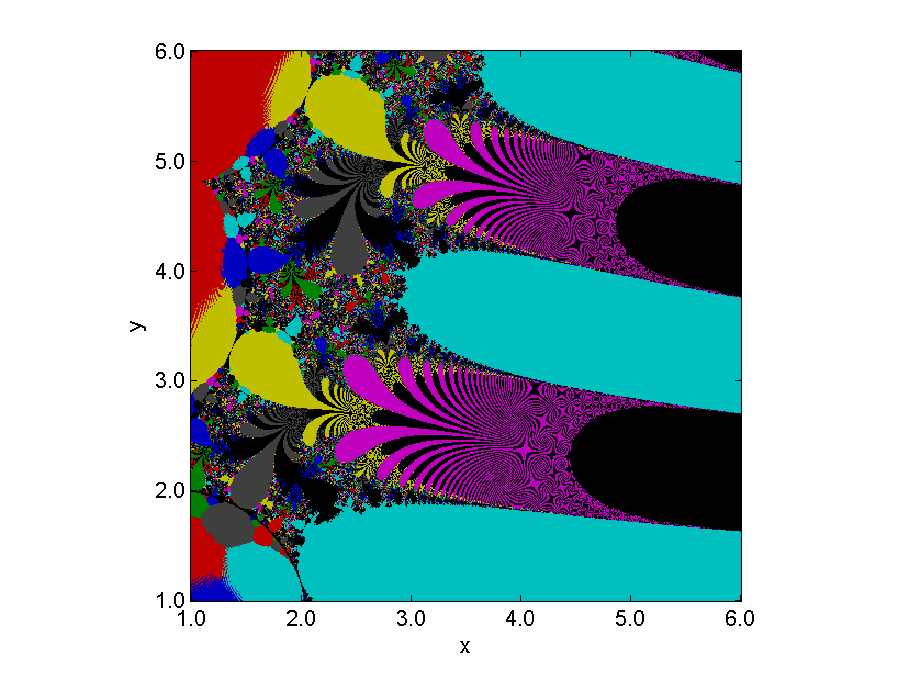
我们最大的区域以原始区域为中心，半宽为30。从原点沿负实轴发出的射线将复平面分割成三分之一，极角为$ pm \frac{\pi}{3}$。所有的分形行为都发生在其中一个隔板附近。不是在分隔符附近开始的迭代收敛到该起始区域的零。用橙色和黄色填充的轮廓和相关的颜色条告诉我们，大多数从距离原点大于30的距离开始的迭代至少需要十几步才能收敛。

分形（F，Fprime，0.30,512）

放大原点

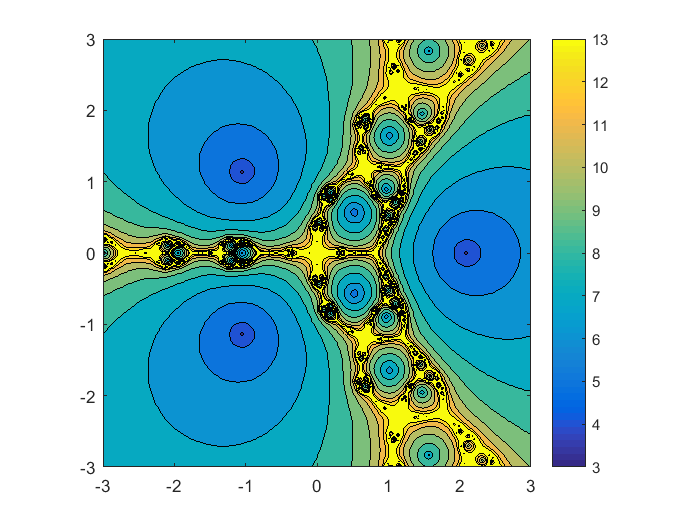
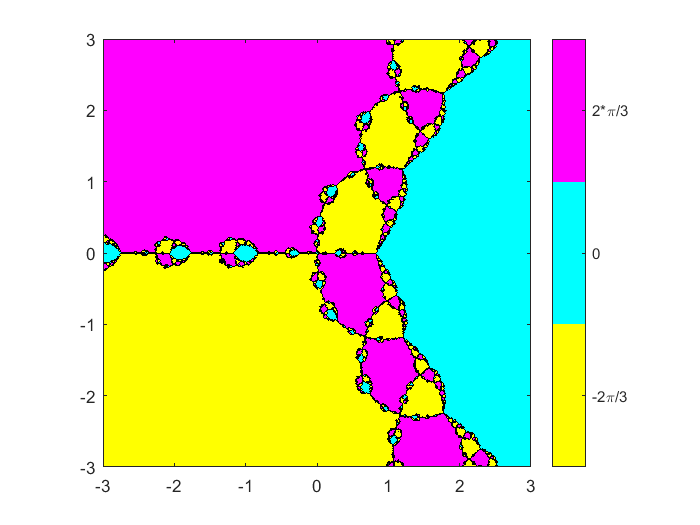
放大10倍。半宽现在是3。函数计数最低的三个蓝色等高线围绕着三个零。这就是牛顿法发挥作用的地方;从接近零开始，迭代将在几个步骤内收敛到那个零。分离三个最小值的区域具有更高的迭代次数和更复杂的行为。当$F'(x) = 3x^2-2$的导数在$$ x = pm \sqrt{\frac{2}{3}} \大约\pm 0.816处为零时，$F'(x)$在分母上有极点。二阶导数$F " (x) = 6x$在原点处为零。等高线图显示了在原点的四向分支模式和在正极的三向分支模式。这两种图案在分形的所有尺度上重复出现。

分形(F Fprime 0, 3512)

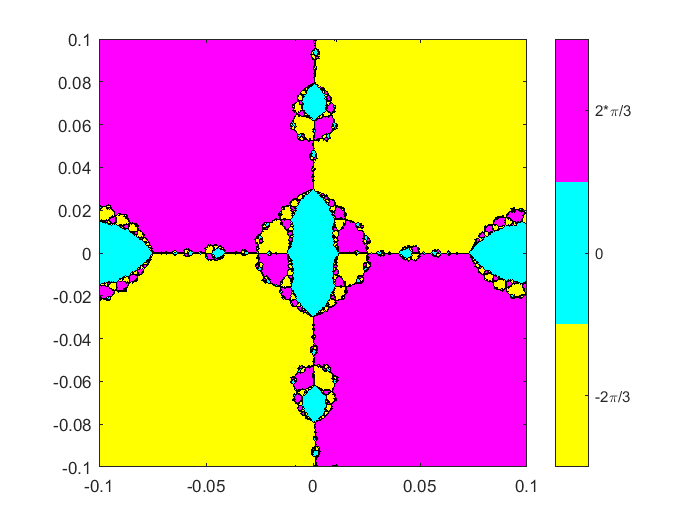
细节在原点。

放大另一个因素30.半宽度现在为0.1。我们可以更详细地看到四向分支模式。在第二轮廓曲线图中，该区域的大部分是洋红色或黄色的大部分，表明大多数迭代会聚到左半平面中的一个复合零中。一个相对较小的部分是彩色青色，表明正实轴上的零收敛较小。

分形（F，Fprime，0,0.1,512）

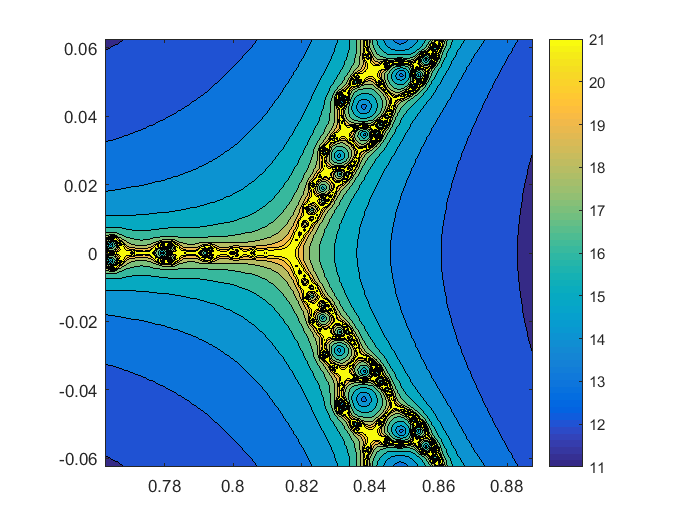
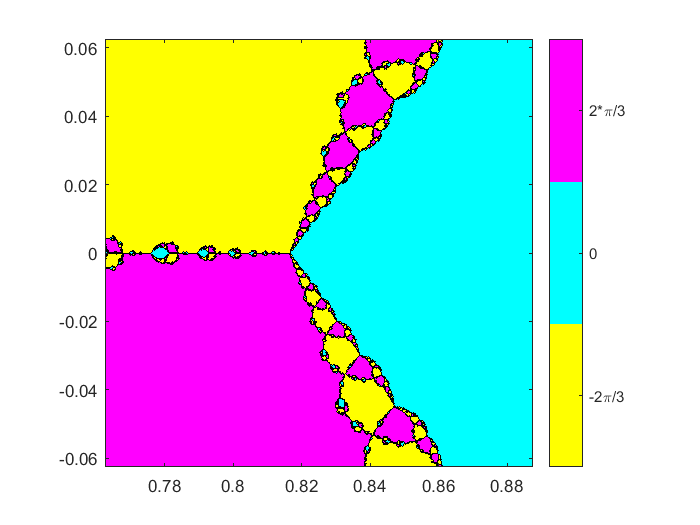
在杆子上

以$x=.816$的价格将平底锅推向极点。我们看到三种颜色，品红，黄和青色，在相同的面积上有一个三向分隔符。从这个极点附近开始的迭代都同样有可能收敛到三个零中的每一个。

分形(F Fprime .825 1/16,512);

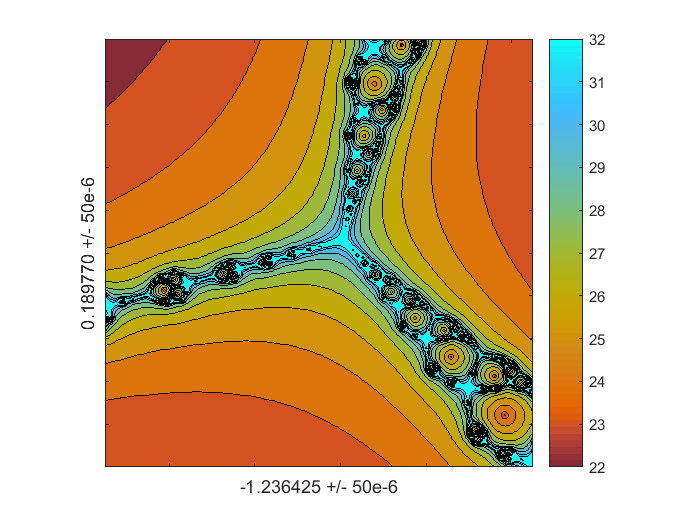
缩放10 ^ 6，翻转colormap

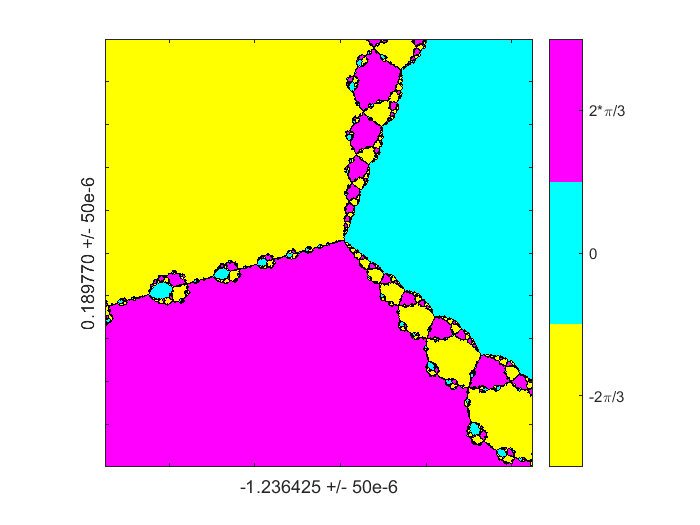
将几乎六个数量级放大到刚刚在负实轴上的复杂平面中的点。我们看到三通分支模式的重复略微旋转。通过互换默认的Colormap中的红色和蓝色的角色，玩颜色很有趣，par．

z0 = -1.236425 + 0.189770i;d = 50e-6;图（1）Colormap（Fliplr（Colormap））;分形(F, Fprime z0 d, 512)标签(“-1.236425”，'0.189770'，'50e-6'）

放大10 ^ 8

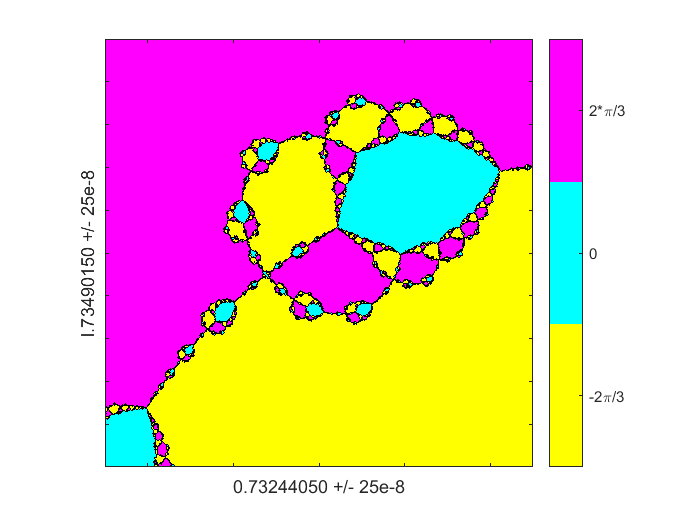
将近八个数量级放大到右半平面上分隔符上的一个点。我们现在拥有三方和四通模式，虽然它们具有不同的颜色，因为我翻了一转Colormap。

z0 = 0.73244050 + 1.73490150我;d = 25 e-8;分形(F, Fprime z0 d, 512)标签('0.73244050'，'L.73490150'，“25 e-8”）

多一个

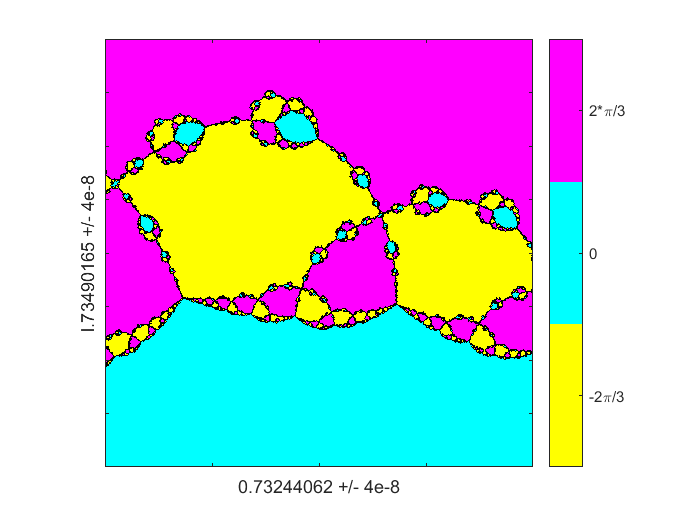
这是我的最后一个。请注意，迭代计数增加到至少25次。尽管牛顿的方法需要更长时间融合，但我们仍然看到了相同的三路和四路径的分支行为模式。

Z0 = 0.73244062 + 1.73490165i;d = 4e-8;图（1）Colormap（铜）;分形(F, Fprime z0 d, 512)标签('0.73244062'，'L.73490165'，“4 e-8”）

参考文献

牛顿方法的整体行为的分形性质是众所周知的。如果你问谷歌关于“牛顿分形”的问题，你会得到很多有趣的链接。看看图片和电影。如果你问“MATLAB牛顿分形”，你会得到几个有趣的链接，包括对MATLAB中心的一些贡献。我真的很喜欢分形。我已经写过Mandelbrot集在与MATLAB实验．我也写了一个博客帖子两年前关于幂塔中循环生成的分形函数$$ z^{z^{z^z}} $$

获取MATLAB代码发布与MATLAB®R2015a