Zeroin,第2部分:布伦特的版本
Richard Brent对Dekker的改进零点算法在1971年发布,使浮点算法更快,更安全,并保证不会失败。
在每次迭代时,选择是由四个可能的步骤进行的:
这是一个有点杂乱的情节,其显示了大多数这些可能性。三个价值$ a $,$ b $和$ c $绘制黑色。函数$$ f(x)= x ^ 3 - 3 x - 2 $$绘制浅灰色,强调算法到目前为止只评估了三次,以给出圆圈所示的三个值。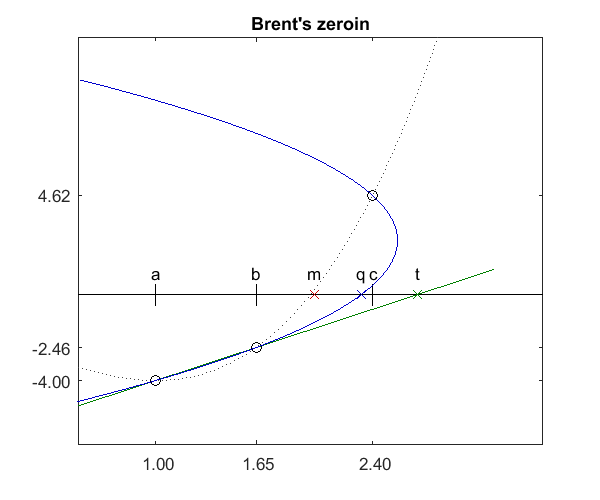 绿线是$ A $和$ B $确定割线。割线步骤将去绿色$ \ $时间标记$ T $,但外面的间隔,这样的零点不会去那里。实际上布伦特人零点在这种情况下,甚至不会考虑割线,因为$ a $和$ c $截然不同。蓝色曲线是按照三个圆圈的$ y $ quadativatic。它在蓝色$ \ times $标有$ q $的蓝色$ \ times $ x $ x。这将是IQI步骤。但是,在这种情况下,$ Q $从$ B $到$ C $的方式超过四分之三,所以布伦特将选择分数。红色$ \ times $标记为$ m $是$ b $和$ c $之间的二分位。值为2.025,它恰好在2.幸运的镜头时真正接近零。
绿线是$ A $和$ B $确定割线。割线步骤将去绿色$ \ $时间标记$ T $,但外面的间隔,这样的零点不会去那里。实际上布伦特人零点在这种情况下,甚至不会考虑割线,因为$ a $和$ c $截然不同。蓝色曲线是按照三个圆圈的$ y $ quadativatic。它在蓝色$ \ times $标有$ q $的蓝色$ \ times $ x $ x。这将是IQI步骤。但是,在这种情况下,$ Q $从$ B $到$ C $的方式超过四分之三,所以布伦特将选择分数。红色$ \ times $标记为$ m $是$ b $和$ c $之间的二分位。值为2.025,它恰好在2.幸运的镜头时真正接近零。>乔治·福赛斯,迈克尔·马尔科姆和克里夫·莫勒尔,对于数学计算的计算机方法,普伦蒂斯霍尔,259pp,1977。发布与Matlab®R2015A
内容
理查德布伦特
理查德·布兰特在1968年至1971年在计算机科学专业的研究生在斯坦福大学。他写了一博士在乔治·福赛斯的方向论文题目算法查找的功能的零和极值而不计算衍生物。我正好是在斯坦福大学的访问教授,是布伦特委员会。福赛斯是一个重要的系列由Prentice-Hall出版的计算机科学书籍的编辑。他因此与布伦特的论断深刻的印象,他发表它的一系列基本持平于1973年与冠军无衍生物的最小化算法。三个重要的算法,布伦特的书中被描述。该算法找到一个真正的变量,函数的零点是一个继任者德克尔的零点,今天仍在Matlab中使用。这是我想在这里写下的算法。另外两个算法,用于最小化一个真实变量的函数,一个用于最小化几个真实变量的函数不再在广泛的应用中。零点的弱点
的版本零点这是由德克尔提出和我描述本系列的第1部分优雅而简洁,但不是万无一失。它有多个根源有问题。一个简单的例子是由$$ f(x)= x ^ 3 $$提供的,如果我们从跨越原点的对称间隔开始,初始剪辑步骤完全击中零,但停止标准无法识别良好的运气。代码需要一个最小的步骤,在这种情况下EPS * realmin,尽可能小的非正规正常的浮点数。这将从根本上永远继续下去,不可能采取小步骤。f = @(x)x。^ 3;
Zeroin(F,-1,1)
1初始-1.00000000000000000000000000000000000000000000000000000000000000000000000000000000/10000000000000000000000324 -0.00000000000000000E + 00 6最小-1.482196937523740E-323 -0.0000000000000000000年+ 00 7 MINIMAL -1.97626258334986262583364980CE + 00 8 MINALAL -2.470328229206060000000年+ 00 8 80000000000000000 + 00 8.0.0000000000000000000年+ 00。。。12341最小-6.095781938389300e-320 -0.000000000000000e + 00 12342最小-6.096276004035141e-320 -0.000000000000000e + 00 12343最小-6.096770069680982e-320 -0.000000000000000e + 00 12344最小-6.097264135326824e-320 -0.000000000000000e + 00。。。关于原点不对称的起始间隔不起作用更好。我们没有完全击中零,所以我们暂时采取一些小的剪辑步骤。但最终我们反复陷入困境,逐步逐步陷入困境,并在圆周OFF中制作圆周交。
zeroin(F, - 5,1)
1初始-5.000000000000000e-01 -1.250000000000000e-01 2初始1.000000000000000e + 00 1.000000000000000e + 00 3正割-3.333333333333334e-01 -3.703703703703705e-02 4正割-2.631578947368422e-01 -1.822423093745445e-02 5割线-1.951779563719863E-01 -7.435193904825083e-03 6正割-1.483300289942098e-01 -3.263527261310824e-03 7正割-1.116805310361257e-01 -1.392940003647091e-03 8正割-8.438934127192455e-02 -6.009838348927866e-04。。。124正割-5.752411316818776e-16 -1.903486478002247e-46 125最小-5.752411316818775e-16 -1.903486478002246e-46 126正割-4.143774132574865e-16 -7.115218233323205e-47 127最小-4.143774132574865e-16 -7.115218233323202e-47 128最小-4.143774132574864e-16 -7.115218233323200e-47 129最小-4.143774132574864e-16 -7.115218233323197e-47 130最小-4.143774132574863e-16 -7.115218233323194e-47 131最小-4.143774132574863e-16 -7.115218233323192e-47 132最小-4.143774132574862E-16 -7.115218233323189e-47。。。
两种改进
为避免这些困难,Brent对Dekker的算法进行了两个重要的改进。一个是检查是否发现了确切零的检查。另一个是介绍变量E.在下面的代码中,在两个连续步骤中跟踪步长比率。该变量参与了关于是否使用二分配的选择。结果,布伦特的算法从来没有超过单独的二分层的两倍以上。让我们看看这些改进如何影响我们的示例Fzero.。选择= OptimSet('展示'那'iter')从归心的间隔开始,精确零点导致早期终止。
Fzero(f,[ - 1,1],选择)
FUNC计数X F(x)的步骤2 1 1初始3 0 0平分
零成立在这间隔[-1,1]ANS = 0从一个不居中的间隔开始,迭代以合理的步骤终止。
Fzero(f,[ - 。5,1],选择)
Func-count x f(x)步骤2 -0.5 -0.125初始3 -0.333333 -0.037037插值4 -0.265664 -0.0187499插值5 -0.197929 -0.007754插值6 -0.197929 -0.007754 Bisection 7 -0.133649 -0.00238724插值。。。151 -4.51944E-16 -9.2311E-47插值152 -7.85458E-18 -4.84584E-52插值153 -7.85458E-18-18 -4.8584E-52平等154 -7.85458E-18-18-4.84584E-52插值
零成立在这间隔[-0.5,1]ans = -7.854580142952130e-18
穆勒的方法
在迭代过程中,我们经常有三个不同的$ x $的值,即$ a $,$ b $和$ c $,以及相应的函数值,$ f(a)$,$ f(b)$。和$ f(c)$。我们可以用二次以$ x $互连这三个值,找到这种二次的根源,并拿到最接近我们最佳近似的根源,以至于下一个近似为$ f(x)$的零。这是Muller的方法。麻烦是二次的根源可能是复杂的。如果我们正在寻找复杂的解决方案,这将是一个优势,并且在这种情况下通常使用Muller的方法。金宝搏官方网站但我们不希望他们在这里,布伦特选择做别的事情。逆二次插值
相反,在$ X $二次的,我们可以在$ Y $的二次函数内插三个点。这是一个``侧身 '' 抛物线,$ P(Y)$,通过内插条件$$ A = P(F(a))的,\ B = P(F(B)),\ C = P(F确定(c))的$$此抛物线总是相交的$ X $轴,它是$ y = 0的$。所以,$ X = P(0)$是下一个迭代。这种方法被称为反二次插值,缩写IQI。这是一个天真的实现,说明了这个想法。它用polyinterp, 取自MATLAB的数值计算类型Iqi.
function x = iqi(f,a,b,c) while abs(c-b) > eps(abs(b)) x = polyinterp([f(a),f(b),f(c)],[a,b,c],0); disp(x) a = b; b = c; c = x; end end这种简单代码的一个难度是多项式插值需要横坐标,在这种情况下是F(a)$,$ f(b)$和$ f(c)$,以截然不同。我们无法保证他们是。例如,如果我们尝试计算$ \ sqrt {2} $使用$ f(x)= x ^ 2 - 2 $并以$ a = -2,b = 0,c = 2 $开头,我们开始了$ f(a)= f(c)$和第一步未定义。如果我们从这个奇异的情况靠近这个奇异的情况,请用$ a = -2.001,b = 0,c = 1.999 $,下一个迭代接近$ x = 500 $。所以IQI一旦靠近零,IQI会比割线更快地收敛,但其全球行为是不可预测的。它需要与二分配合并以具有可靠的算法。
布伦特的算法
喜欢Dekker的原始版本,Brent的版本零点开始以一定间隔$ [A,B] $该函数$ F(X)$改变符号。目标是间隔减少到一个很小的子间隔在其上仍函数改变符号。变量$ A $,$ B $和$ C $起到同样的作用:- 到目前为止,$ B $是最佳零,从此感觉到$ f(b)$是迄今为止$ f(x)$的最小值。
- $ a $是$ b $的前值,所以$ a $和$ b $ mails megain。
- $ C $和$ B $括号标志更改,所以$ B $和$ C $提供中点。
- 如果$ a \ ne c $,请尝试反转二次插值。
- 如果$ a = c $,请尝试剪切插值。
- 如果插值步骤靠近端点,或间隔之外,请使用二分配。
- 如果步骤小于容差,请使用公差。
ZeroIn_plot(1,2.4)
 绿线是$ A $和$ B $确定割线。割线步骤将去绿色$ \ $时间标记$ T $,但外面的间隔,这样的零点不会去那里。实际上布伦特人零点在这种情况下,甚至不会考虑割线,因为$ a $和$ c $截然不同。蓝色曲线是按照三个圆圈的$ y $ quadativatic。它在蓝色$ \ times $标有$ q $的蓝色$ \ times $ x $ x。这将是IQI步骤。但是,在这种情况下,$ Q $从$ B $到$ C $的方式超过四分之三,所以布伦特将选择分数。红色$ \ times $标记为$ m $是$ b $和$ c $之间的二分位。值为2.025,它恰好在2.幸运的镜头时真正接近零。
绿线是$ A $和$ B $确定割线。割线步骤将去绿色$ \ $时间标记$ T $,但外面的间隔,这样的零点不会去那里。实际上布伦特人零点在这种情况下,甚至不会考虑割线,因为$ a $和$ c $截然不同。蓝色曲线是按照三个圆圈的$ y $ quadativatic。它在蓝色$ \ times $标有$ q $的蓝色$ \ times $ x $ x。这将是IQI步骤。但是,在这种情况下,$ Q $从$ B $到$ C $的方式超过四分之三,所以布伦特将选择分数。红色$ \ times $标记为$ m $是$ b $和$ c $之间的二分位。值为2.025,它恰好在2.幸运的镜头时真正接近零。Fzero.
Brent包括本书中该算法的Algol和Fortran实现。Forsythe,Mike Malcolm,我使Fortran计划为零发现章节的基础对于数学计算的计算机方法。代码是仍然可以从netlib获得。我们命名为matlab版本Fzero.。这里是教材版本,fzerotx, 从MATLAB的数值计算。这不是所有的matlabFzero.。在我的下一篇博客,我会处理,需要知道该函数改变符号的间隔。类型fzerotx
function b = fzerotx(f,ab,varargin)fzero的pertotx教科书版本。%x = fzerotx(f,[a,b])试图在a和b之间找到f(x)的零。%f(a)和f(b)必须具有相反的迹象。Famedotx返回一个单个[a,b]的小子内部的一个%终点,其中f更改符号。超出前两个的%参数,从Fzerotx(f,[a,b],p1,p2,...),%通过f(x,p1,p2。)。%%示例:%fatzotx(@sin,[1,4])%f = @(x)sin(x);福利克(F,[1,4])%Copyright 2014 Clyver%版权所有2014 MathWorks,Inc.%初始化。a = ab(1);b = ab(2);fa = f(a,varargin {:}); fb = F(b,varargin{:}); if sign(fa) == sign(fb) error('Function must change sign on the interval') end c = a; fc = fa; d = b - c; e = d; % Main loop, exit from middle of the loop while fb ~= 0 % The three current points, a, b, and c, satisfy: % f(x) changes sign between a and b. % abs(f(b)) <= abs(f(a)). % c = previous b, so c might = a. % The next point is chosen from % Bisection point, (a+b)/2. % Secant point determined by b and c. % Inverse quadratic interpolation point determined % by a, b, and c if they are distinct. if sign(fa) == sign(fb) a = c; fa = fc; d = b - c; e = d; end if abs(fa) < abs(fb) c = b; b = a; a = c; fc = fb; fb = fa; fa = fc; end % Convergence test and possible exit m = 0.5*(a - b); tol = 2.0*eps*max(abs(b),1.0); if (abs(m) <= tol) | (fb == 0.0) break end % Choose bisection or interpolation if (abs(e) < tol) | (abs(fc) <= abs(fb)) % Bisection d = m; e = m; else % Interpolation s = fb/fc; if (a == c) % Linear interpolation (secant) p = 2.0*m*s; q = 1.0 - s; else % Inverse quadratic interpolation q = fc/fa; r = fb/fa; p = s*(2.0*m*q*(q - r) - (b - c)*(r - 1.0)); q = (q - 1.0)*(r - 1.0)*(s - 1.0); end; if p > 0, q = -q; else p = -p; end; % Is interpolated point acceptable if (2.0*p < 3.0*m*q - abs(tol*q)) & (p < abs(0.5*e*q)) e = d; d = p/q; else d = m; e = m; end; end % Next point c = b; fc = fb; if abs(d) > tol b = b + d; else b = b - sign(b-a)*tol; end fb = F(b,varargin{:}); end
参考
理查德·P·布伦特,“用查找功能的零保证收敛的算法,”电脑杂志14,422-25,1971年理查德·P·布伦特,无衍生物的最小化算法,新泽西州的Prentice-Hall,New Jersy,1973年,195年PP。由Dover,纽约,2002年和2013年转载。
|














 克利夫的角落:克里夫·莫勒尔对数学和计算机
克利夫的角落:克里夫·莫勒尔对数学和计算机 Loren在Matlab的艺术上
Loren在Matlab的艺术上 史蒂夫在图像处理与matlab
史蒂夫在图像处理与matlab Simulin金宝appk上的家伙
Simulin金宝appk上的家伙 深度学习
深度学习 开发人员区域
开发人员区域 斯图尔特的MATLAB视频
斯图尔特的MATLAB视频 新闻标题背后
新闻标题背后 文件本周交易所选择
文件本周交易所选择 汉斯在某种程度上
汉斯在某种程度上 学生休息室
学生休息室 初创公司,加速器和企业家
初创公司,加速器和企业家 MATLAB社区
MATLAB社区 matlabユーザーコミュニティー
matlabユーザーコミュニティー



注释
要发表评论,请点击这里在您的帐户MathWorks公司签署或创建一个新的。