(请将昨天(11月28日)的错误帖子替换为更正后的版本。)

这是一个很短的线性代数课程。奇异值分解为吉尔·斯特朗的四基本子空间提供了一个自然的基础。

截图来自Gil Strang MIT/MathWorks视频讲座，《线性代数概貌》．

内容

吉尔斯特朗

吉尔·斯特朗告诉我，他在20世纪70年代开始从四个基本子空间的角度思考线性代数当时他写了第一版教材，线性代数概论．去年5月出版的第五版以这些空间为特色在封面上．

这个概念是他作品的核心视频讲座麻省理工学院18.06课程。它甚至进入了新视频系列关于我和他为MIT和MathWorks做的常微分方程他的论文收录在18.06的注释中，参考如下。

四个子空间

假设$A$是一个$m × $n$的矩阵，它将$R^n$中的向量映射到$R^m$中的向量。与$A$相关的四个基本子空间，两个在$R^n$中，两个在$R^m$中，分别是:

行空间和零空间是正交并张成整个R^n。列空间和左零空间也是正交并张成整个R^m。

维度和等级。

的维子空间的向量是线性无关的向量的个数，以张成空间。线性代数基本定理是

换句话说，线性无关的行数等于线性无关的列数。这似乎是显而易见的，但实际上这是一个需要证明的微妙事实。

的排名矩阵的向量是线性无关的行数或列数。

奇异值分解

四个基本子空间的自然基由$A$的奇异值分解(SVD)提供。

$$ A = U \Sigma V^T $$

矩阵$U$和$V$是正交．

$$ U^T U = I_m， \ \ V^T V = I_n $$

你可以把正交矩阵看作是二维旋转的多维推广。矩阵$\Sigma$是对角，所以它只有非零元素在主对角线上。

这些矩阵的形状和大小很重要。矩阵$A$是矩形的，有$m$行和$n$列;$U$是方形的，与$A$的行数相同;$V$也是方形的，列数与$A$相同;$\Sigma$与$A$大小相同。这是这个方程的图片，当$ a $又高又瘦，那么$m > n$。$\Sigma$的对角线元素是奇异值，显示为蓝点。$\Sigma$的所有其他元素都是零。

$U$和$V$中的符号和列的顺序总是可以使奇异值是非负的，并按递减顺序排列。

对于任何像$\Sigma$这样的对角线矩阵，很明显，秩(即独立行或列的数量)就是非零对角线元素的数量。

在MATLAB中，SVD由语句计算。

[U,Sigma,V] = svd(A)

对于不精确的浮点计算，将秩取为的数是合适的不可忽视的对角线元素。这个函数

r = rank(A)

计数大于容差的奇异值的数目。

两个子空间

右边$A = U\Sigma V^T $两边同时乘以$V$。由于$V^T V = I$，我们发现

$$ AV = U\Sigma $$

这是照片。我在列$r$后面画了一条绿线来显示排名。$\Sigma$的唯一非零元素，即奇异值，是蓝点。

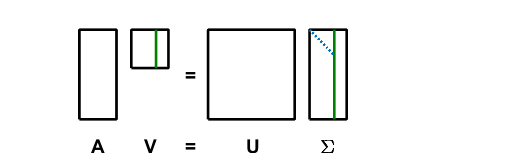
一列一列地写出这个方程。

$$ Av_j = \sigma_j u_j， \ \ j = 1，…, r $ $

$$ Av_j = 0， \ \ j = r+1，…n $ $

这就是说$A$将$V$的前$r$列映射到$U$的前$r$列的非零倍数，并将$V$的剩余列映射到零。

还有两个子空间

转置方程$A = U\Sigma V^T $，并在右边两边乘以$U$。由于$U^T U = I$，我们发现

$$ U = V \Sigma^T $$

这是图片，在等级处有绿线。

一列一列地写出来。

$$ A^T u_j = \sigma_j v_j， \ \ j = 1，…, r $ $

$$ A^T u = 0， \ \ j = r+1，…, m $ $

这就是说$A^T$将$U$的前$r$列映射到$V$的前$r$列的非零倍数，并将$U$的剩余列映射到零。

四行

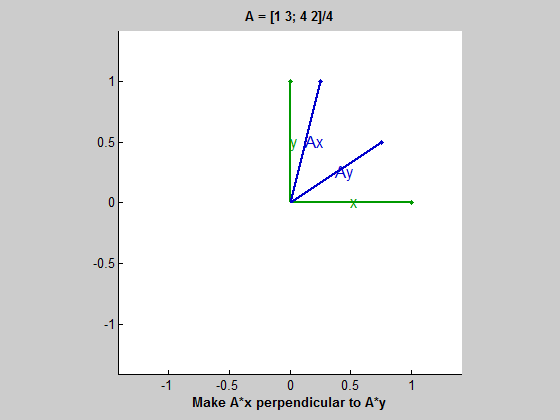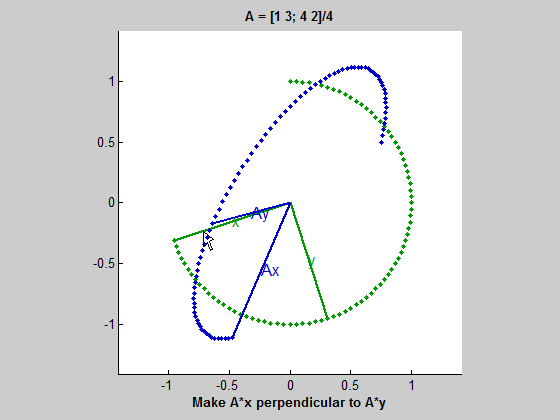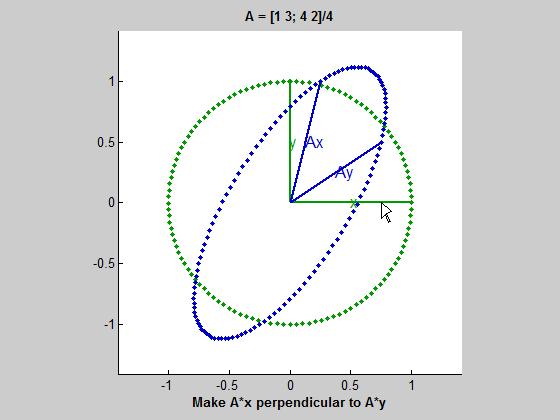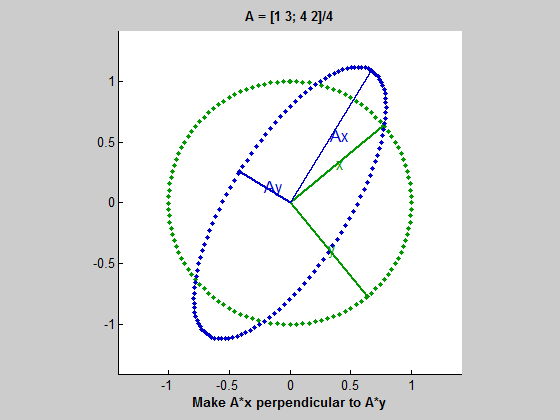
这是一个涉及二维直线的例子，因此$m = n = 2$。从这些向量开始。

U = [-3 4]' v = [1 3]'

U = -3 4v = 1

矩阵A是它们的外积。

A = u*v'

A = -3 -9 4 12

计算SVD。

[U,Sigma,V] = svd(A)

U = -0.6000 0.8000 0.8000 0.6000 Sigma = 15.8114 000 V = 0.3162 -0.9487 0.9487 0.3162

正如预期的那样，$\Sigma$只有一个非零奇异值，因此秩为$r = 1$。

左边和右边的第一个奇异向量是我们的起始向量，标准化为单位长度。

Ubar = u/范数(u) vbar = v/范数(v)

Ubar = -0.6000 0.8000 vbar = 0.3162 0.9487

$A$的列彼此成比例，并且与$\bar{u}$成比例。所以列空间就是由任意一列的倍数生成的直线$\bar{u}$是列空间的规范化基向量。$A^T$的列彼此成比例，并且与$\bar{v}$成比例。$\bar{v}$是行空间的规范化基向量。

唯一的非零奇异值是归一化因子的乘积。

σ =范数(u)*范数(v)

Sigma = 15.8114

第二个左右奇异向量，即$V$和$U$的第二列，为$A$和$A^T$的零空间提供基底。

这是照片。

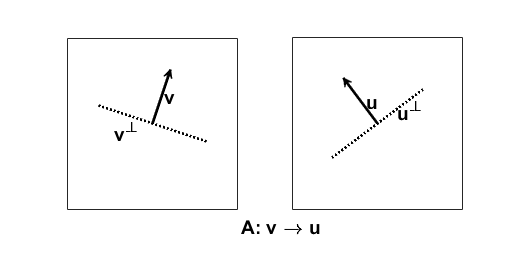
参考文献

吉尔伯特·斯特朗，《四基本子空间:四条线》，麻省理工学院课程18.06的未标注笔记，< http://web.mit.edu/18.06/www/Essays/newpaper_ver3.pdf>

吉尔伯特-斯特朗,线性代数概论韦尔斯利-剑桥出版社，2016年第五版，x+574页，< http://bookstore.siam.org/wc14>

吉尔伯特·斯特朗，《线性代数基本定理》美国数学月刊，第100卷第9期。(1993年11月)，第848-855页，< http://www.jstor.org/stable/2324660?seq=1 page_scan_tab_contents>，也可以在< http://www.souravsengupta.com/cds2016/lectures/Strang_Paper1.pdf>

获取MATLAB代码

发布与MATLAB®R2016b