维基百科的文章帕斯卡三角形数以百计的三角形的性质,有几十种其他网页致力于它。这里有一些事实,我发现最有趣的。

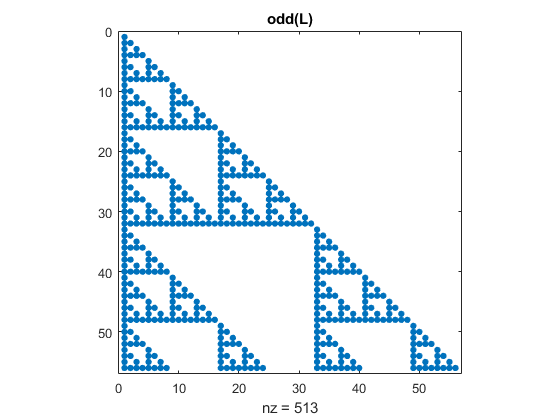
内容

布莱斯•帕斯卡

布莱斯•帕斯卡(1623 - 1662)是一位17世纪的法国数学家,物理学家,发明家和神学家。他的行程du三角形arithmetique(论述算术三角形)于1665年在他死后出版。但这并不是第一个出版的三角形。不同版本出现在印度、中国、波斯、意大利和其他手稿世纪之前帕斯卡。

二项式系数

的二项式系数通常用$ {n} \选择{k}的多种方式选择k美元无序的结果从$ n美元的可能性。这些系数出现在二项的扩张(x + 1) ^ n美元。例如,当n = 7美元

信谊xn = 7;x7 =扩大((x + 1) ^ n)

x7 = x ^ 7 + 7 * x ^ 6 + 21 * x ^ 5 x ^ 4 + + 35 * 35 * x ^ 3 + 21 * x ^ 2 + 7 * x + 1

在形式上,二项式系数是由$ $ {{n} \选择{k}} = \压裂{n !}{k !(n - k) !}$ $但过早的阶乘的浮点数溢出使这种不能令人满意的基础计算。一个更好的方法采用递归$ $ {{n} \选择{k}} = {{n} \选择{k}} + {{n} \选择{k - 1}} $ $这是使用MATLAB函数nchoosek (n, k)。

帕斯卡矩阵

MATLAB提供了两个帕斯卡矩阵。一是对称的,正定,antidiagonals二项式系数。

P =帕斯卡(7)

P = 1 1 1 1 1 1 1 1 2 3 4 5 6 7 1 3 6 10 15 21 28 1 4 10 20 35 56 84 1 5 15 35 70 126 210 1 6 21 56 7 28 126 252 462 84 210 462 924

另一个下三角,二项式系数的行。(我们将会看到为什么甚至编号列有负号。)

L =帕斯卡(7,- 1)

L = 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 2 1 0 0 0 0 1 3 3 1 0 0 0 1 4 6 0 0 1 5 -10 5 1 0 1 6 15 -20 15 6 1

单独的元素

P (i, j) = P (j, i) = nchoosek (i + j2, j - 1)

(暂时忽略负号)我通用电气\美元j

L (i, j) = nchoosek (j - 1张)

第一个有趣的事实是,l柯列斯基因素(低)P。

L =胆固醇(P)的

L = 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 2 1 0 0 0 0 1 3 3 1 0 0 0 1 4 6 0 0 1 5 10 10 5 1 0 1 6 15 20 15 6 1

所以我们可以重建P从l。

P = L * L '

P = 1 1 1 1 1 1 1 1 2 3 4 5 6 7 1 3 6 10 15 21 28 1 4 10 20 35 56 84 1 5 15 35 70 126 210 1 6 21 56 7 28 126 252 462 84 210 462 924

帕斯卡三角形

传统的帕斯卡三角形是通过P顺时针旋转45度,或向右滑动的行L在增量的一半。的每个元素生成的三角形是两个以上的总和。

triprint(左)

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

√标识

甚至当编号列l给出负号矩阵成为身份的平方根。

L =帕斯卡(n, 1) L_squared = L ^ 2

L = 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 2 1 0 0 0 0 1 3 3 1 0 0 0 1 4 6 0 0 1 5 -10 5 1 0 1 6 15 -20 15 6 1 L_squared = 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

这是一个锻炼你。是什么√眼(n))吗?为什么它不是l吗?

立方根的身份

当我第一次看到这个,我很惊讶。L逆时针旋转。结果是一个身份的立方根。

X = rot90 (L, 1) X_cubed = X ^ 3

X = 1 1 1 1 1 1 1 6 5 4 3 2 1 0 15 10 6 -20 -10 4 1 1 0 0 0 0 0 15 5 1 0 0 0 0 6 1 1 0 0 0 0 0 0 0 0 0 0 0 X_cubed = 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

Sierpinski

二项式系数是奇怪的?这是一个羽翼未丰的分形。

奇怪的= @ (x)国防部(x, 2) = = 1;n = 56;L = abs (pascal (n, 1));间谍(奇数(L))标题(“奇(左)”)

斐波那契

总结antidiagonals的l斐波纳契数列。

n = 12;一个= fliplr (abs (pascal (n, 1)))为k = 1: n F (k) =总和(诊断接头(A, n - k));结束F

= 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 1 3 3 1 0 0 0 0 0 0 0 1 4 6 0 0 0 0 0 0 1 1 5 10 10 5 0 0 0 0 0 1 6 15 20 15 6 1 0 0 0 0 1 7 21 35 35 21 7 1 0 0 0 1 8 28 56 70 56 28 8 1 0 0 1 9 36 84 126 126 84 36 9 1 0 1 45 120 210 252 210 120 45 10 1 11 55 165 330 462 462 330 165 55 11 F = 1 1 2 3 5 8 13 21 34 55 89 144

π

第三列中的元素的下三角矩阵是帕斯卡三角形数。第n个三角形数的数量在第n个保龄球保龄球的行数组。$ $ t_n = {{n + 1} \选择{2}}$ $

L =帕斯卡(12日1);t = L(3:最终,3)'

t = 1 3 6 10 15 21 28 36 45 55

这是一个不寻常的系列相关\π美元的三角形数。迹象去+ +——+ + - - - - - - -。

π- 2 = 1 + 1/3 - 1/6 - 1/10 + 1/15 + 1/21 - 1/28 - 1/36 + 1/45 + 1/55 -…

类型pi_pascal

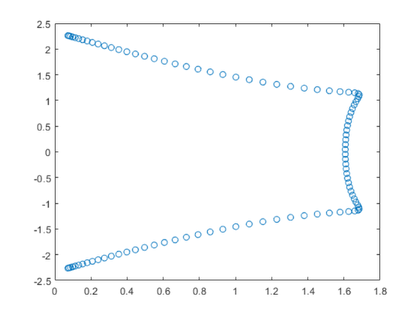
功能派= pi_pascal (n) tk = 1;s = 1;k = 2: n tk = tk + k;如果国防部(k + 1, 4) > 1 s = s + 1 / tk;其他s = s - 1 / tk;结束结束饼= 2 + s;

一千万条款给\π小数点后14美元。

格式长派= pi_pascal(10000000)呃=π-派

派= 3.141592653589817呃= -2.398081733190338 e-14

矩阵指数

最后,我喜欢这一个。解决(可能无限)的一组常微分方程$ \点{x_1} = x_1 $ $ \点{x_j} = x_j + (j - 1)间的{j - 1} $ $ x_j = e t (t + 1) ^ ^ {j - 1} $这意味着简单的对角矩阵的矩阵指数

D =诊断接头(1:7,1)

D = 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 7 0

是

expm_D =圆(expm (D))

expm_D = 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 1 3 3 1 0 0 0 0 1 4 6 0 0 0 1 1 5 10 10 5 0 0 1 6 15 20 15 6 1 0 1 7 21 35 35 21 7 1

谢谢

感谢尼克•海厄姆pascal.m,gallery.m和28.4节的n . j·海厄姆准确性和稳定性的数值算法第二版,暹罗,2002年。http://epubs.siam.org/doi/book/10.1137/1.9780898718027

得到了MATLAB代码

发表与MATLAB®R2018a