这是第三次在一系列的文章有限傅里叶变换。傅里叶矩阵产生一个有趣的图形和令人吃惊的特征值分布。

内容

傅里叶矩阵

秩序的傅里叶矩阵n n——美元,美元$ n元素的复杂范德蒙矩阵F $美元$ F {k, j} $ n th根美元的权力的统一$ $ \ω= e ^{2 \π/ n} $ $ $ $ F {k, j} = \ω^ {k j} $ $可以生成矩阵与MATLAB语句

k = (0: n - 1);j = (0: n - 1);F = exp(2 *π*我* * j k / n);

或者,通过FFT的单位矩阵

F = fft(眼(n))

该声明

情节(F)

连接在复平面上点的坐标的实部和虚部的列的元素F,从而生成一个图的子图n点。如果n是质数,连接所有列的元素生成完整的图吗n点。如果n不是质数,稀疏图的所有列的相关的计算复杂度,因此速度,快速FFT算法。的图n= 8、9、10和11是由以下代码生成和绘制。

为n = 8:11次要情节(2,2,n-7) F = fft(眼(n));情节(F)轴广场轴从标题([“n =”int2str (n))结束

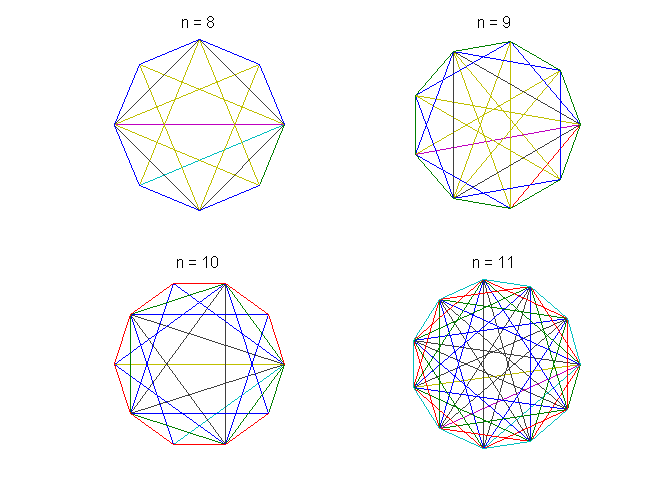
因为n = 11是质数,相应的图表显示所有可能的连接。但是其他三个值n不是美元的'图是失踪的一些链接,说明向量与许多点的FFT计算速度更快。

n = 12

这篇文章的其余部分了F12更多细节。这是它的图形。

clf n = 12;F = fft(眼(n));情节(F)轴广场轴从标题([“n =”int2str (n))

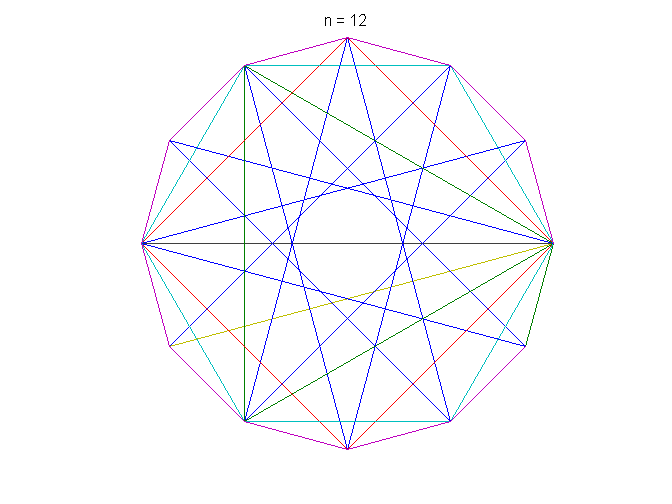
fftmatrix

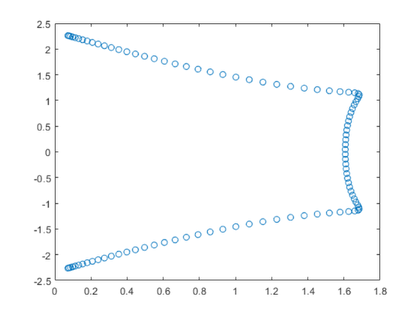
这个项目fftmatrix,可以在这里,或包含在不合格品程序,允许您在调查这些图表。fftmatrix (n)情节的傅里叶矩阵的列顺序n。fftmatrix (n, j)情节只是一列。让我们画出单个的列F12。第一列的F12是所有的,所以它的情节只是一个单点。

为j = 1:12 p =国防部(j - 1 4) + 1;次要情节(2,2,p);fftmatrix_mod (j - 1)标题([“j = 'int2str (j)))如果snapnow p = = 4,结束结束

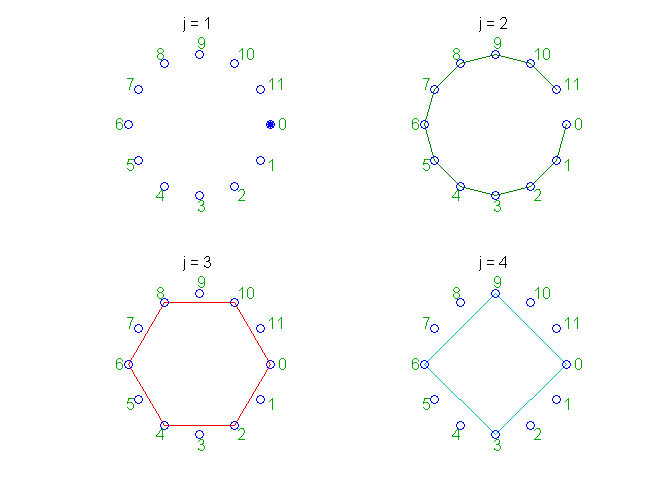
典型的行为,看看第三次要情节,标记红色的图j = 3,第三列生成的

F (: 3)

ans = 1.0000 + 0.0000我0.5000 - 0.8660 -0.5000 - 0.8660 -1.0000 0.5000我-0.5000 + 0.8660 + 0.0000 + 0.8660我1.0000 + 0.0000 0.5000 - 0.8660 -0.5000 - -0.5000 0.8660 -1.0000 + 0.0000我我0.5000 + 0.8660 + 0.8660

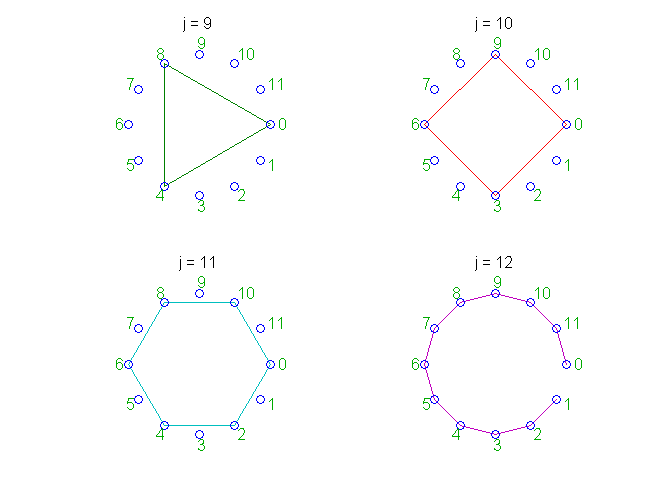
这些都是\ω^ 2美元的权力。因为2分12均匀这些权力打击所有偶数点在圆和所有奇数点小姐的两倍。现在看看青色图标记j = 11。这是美元的权力\ω^{10}$,这是复杂的配合的权力\ω^ 2美元。所以两个图表躺在上面。6的12列的图F12只连接节点的一个子集和十列的谎言之上的复共轭列。因此,当所有的列组合形成完整的图,这是稀疏的。这种稀疏,反过来,可以构建一个快速有限傅里叶变换算法n = 12。

特征值

我一直好奇傅里叶矩阵的特征值和向量。1979年,我的三个朋友在新墨西哥大学的格斯Efroymson,艺术威尔·斯坦·斯坦伯格,暹罗审查问题部分提出同样的问题。他们不知道吉姆·麦克莱伦和汤姆公园实际上已经解决了他们的问题七年前,当吉姆是莱斯大学研究生汤姆下工作。我不了解McClellan-Parks纸直到最近。离散傅里叶变换的维基百科页面说关于特征值是众所周知的事实,但这特征向量是当前的研究课题。让我们重新调节F这样它的列有美元单位长度。

F = F /√(n);

这使得我$ $ F ' \ F =

轮(F ' * F)

ans = 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1

现在F是美元统一的,复杂的泛化正交。这意味着所有的特征值在复平面躺在单位圆。此外,事实证明,F ^ 4 =我美元。

轮(F ^ 4)

ans = 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1

这意味着任何特征值\λ美元必须满足\λ^ 4 = 1美元。因此唯一可能的特征值是1,1,我,我。你可能会猜测,猜测,如果n能被4整除,美元将均匀分布的特征值在这四个值。但是,令人惊讶的是,至少对我来说,这种情况不会发生。

λ= eig (F)

λ= 1.0000 + 0.0000我-1.0000 + 0.0000 -0.0000 -1.0000 + 0.0000 + 1.0000我我-0.0000 + 1.0000 -1.0000 - 0.0000 0.0000 - 1.0000我1.0000 + 0.0000 -0.0000 - 1.0000 1.0000 - 0.0000 1.0000 - 0.0000 0.0000 - 1.0000我

很难选择通过这种无序输出,但有四个+ 1,三个1,三个我的,只有两个+ i。这是一个棘手的代码使用角和稀疏索引数的计数功能的四个可能的特征值的数量。

类型eigfftmat

函数c = eigfftmat (n) % eigfftmat数傅里叶矩阵的特征值。% c = eigfftmat (n)是一个4向量与计数+ 1,1,-,+我。%计算特征值。e = eig (fft(眼(n)));%稀疏重复索引作为一个计数器。c =全(稀疏(mod(圆(角(e ') /(π/ 2)),4)+ 1,1,1));2 c ([3]) = c (3 [2]);结束

当我们运行这个代码的值序列n,我们看到了McClellan-Parks分析预测的模式。的四个可能的特征值的数量取决于地板(n / 4)和国防部(n, 4)。

disp (“n + 1 1 -我+我)为n = 4:20 disp ([n eigfftmat (n)))结束

n + 1 1 -我+我4 2 1 1 5 2 1 1 1 6 2 2 1 1 7 2 2 2 1 8 10 3 2 2 1 9 3 2 2 2 3 3 2 2 11 13 3 3 3 2 12 4 3 2 4 3 3 3 14 4 4 3 3 15 4 4 4 3 16 5 4 3 17 5 4 4 4 18 5 4 20 6 5 4 4 19 5 5 5 5 5 4

麦克莱伦的证明和公园论文涉及到特征向量和相当复杂。事实证明,这个MATLAB表达式

地板((n + [4 2 1 1]) / 4)

生成一个4向量的复合度+ 1,1,-,+我特征值对于任何给定的值n。

引用

j·h·麦克莱伦和t . w .公园、“离散傅里叶变换的特征值和特征向量”,IEEE反式。音频Electroacoust 20, 66 - 74,< http://dx.doi.org/10.1109/TAU.1972.1162342>,1972。g . Efroymson a .威尔和年代。斯坦伯格,”一个矩阵特征值问题”,暹罗审查,21岁,139 - 139,< http://dx.doi.org/10.1137/1021013>,1979。维基百科,“离散傅里叶变换”,< http://en.wikipedia.org/wiki/Discrete_Fourier_transform>,09/03/2014检索。

得到了MATLAB代码发表与MATLAB®R2014a