这是有限傅里叶变换系列文章的第二篇。这篇文章是关于快速FFT算法本身的。一个递归的分治算法实现在一个优雅的MATLAB函数命名ffttx．

目录

FFFT

首字母缩略词FFT模棱两可。第一个F代表“快速”和“有限”。更准确的缩写应该是FFFT，但没有人愿意使用它。在MATLAB中，表达式fft（x）计算任意向量的有限傅里叶变换x. 如果是整数，则计算速度最快n=长度（x）是小素数幂的乘积。

快速傅里叶变换

定义的直接应用

$$Y_k=\sum_{j=0}^{n-1}\omega^{jk}Y_j、\k=0、\ldots，n-1$$

对于$Y$的每个$n$分量，需要$n$的乘法和$n$的加法，总共是$2 n^2$浮点运算。这并不包括$\omega$的幂的生成。一台能够每微秒做一次乘法和加法的计算机需要100万秒，或大约11.5天，才能完成100万点的FFT。

有几个人独立发现了快速FFT算法，许多人后来对其发展做出了贡献，但普林斯顿大学的约翰·图基（John Tukey）和IBM研究院的约翰·库利（John Cooley）1965年的一篇论文被普遍认为是FFT现代用法的起点。

现代快速FFT算法的计算复杂度是$O(n \mbox{log}_2 n)$，而不是$O(n²)$。如果$n$是2的幂，则长度为$n$的一维FFT只需要少于$3 n \mbox{log}_2 n$的浮点运算。对于$n = 2^{20}$，这比$2 n^2$快了将近35000倍。即使$n = 2^{10}$，因子约为70。

使用MATLAB 8.3和2.7 GMHz Intel Core i7笔记本电脑fft（x）如果长度（x）是2^23 = 8388608大约是0.5秒。内置的快速傅里叶变换该函数基于FFTW，“西方最快的傅里叶变换”，由Matteo Frigo和Steven G.Johnson于1998年在麻省理工学院开发。

快速算法

快速FFT算法的关键在于$2n$单位根的平方等于$n$单位根。使用复杂的符号,

$ e^{-2 i/n} $

我们有

$ _{2n}^2 = $ n $

快速算法的推导从有限傅里叶变换的定义开始:

$$Y_k=\sum_{j=0}^{n-1}\omega^{jk}Y_j、\k=0、\ldots，n-1$$

将和除以偶数下标项和奇数下标项。

$$Y\u k=\sum\u{偶数\j}\omega^{jk}Y\u j\+\\sum\u{奇数\j}\omega^{jk}Y\j$$

假设$n$是偶数，$k\leq n/2-1$，并重新调整总和下标的用途。

$$Y_k=\sum_{j=0}{n/2-1}\omega^{2jk}Y{2j}\+\\omega^k\sum{j=0}{n/2-1}\omega^{2jk}Y{2j+1}$$

这两个总和是长度为$n/2$的FFT的组成部分，即带有偶数和奇数下标的$y$部分。为了得到长度为$n$的整个FFT，我们必须做两个长度为$n/2$的FFT，将其中一个乘以$\omega$的幂，然后将结果串联起来。

长度为$n$的FFT和长度为$n/2$的两个FFT之间的关系可以在MATLAB中简洁地表示。

ω= exp(2 *π*我/ n);k = (0: n / 2 - 1);W = ^ k;u = fft (y (1:2: n - 1));v = w。* fft (y (2:2: n));

然后

fft (y) = [u + v;uv];

现在，如果$n$不仅是偶数，而且是2的幂，这个过程可以重复。长度$n$的FFT表示为两个长度$n/2$的FFT，然后是四个长度$n/4$的FFT，然后是八个长度$n/8$的FFT，以此类推，直到我们得到长度为1的$n$ FFT。长度为1的FFT就是数字本身。如果$n = 2^p$，递归的步骤数是$p$。每一步都有$O(n)$ work，所以总工作量是

$$ O(np) = O(n \mbox{log}_2 n

如果$n$不是2的幂，仍然可以用几个更短的FFT来表示长度$n$的FFT。一个长度为100的FFT是两个长度为50的FFT，或四个长度为25的FFT。一个长度为25的FFT可以用5个长度为5的FFT来表示。如果$n$不是质数，则长度为$n$的FFT可以用长度除$n$的FFT来表示。即使$n$是素数，也可以将FFT嵌入到另一个长度可以被分解的序列中。这里我们不详细介绍这些算法。

ffttx

教科书的功能ffttx结合了两个基本思想。如果$n$是2的幂，那么它使用$O（n\mbox{log}\u2n）$快速算法。如果$n$有一个奇数因子，它使用快速递归，直到达到奇数长度，然后建立离散傅里叶矩阵并使用矩阵向量乘法。

ffttx是我最喜欢的MATLAB函数之一。这是完整的代码。

函数y = ffttx(x) %% FFTTX(X)与FFT(X)计算相同的有限傅里叶变换%。对于偶数阶，代码使用递归分治和%征服算法;对于奇数阶，代码使用矩阵-向量%乘法。如果长度(X)是m*p %，其中m是奇数，p是2的幂，这种方法的计算%复杂度是O(m²)*O(p*log2(p))。

x=x（：）；n=长度（x）；ω=exp（-2*pi*i/n）；

如果rem（n，2）=0%递归分治k=（0:n/2-1）'；w=ω。^k；u=ffttx（x（1:2:n-1））；v=w.*ffttx（x（2:2:n））；y=[u+v；u-v]；傅里叶矩阵j=0:n-1；k=j'；F=ω^（k*j）；y=F*x；终止

傅里叶矩阵

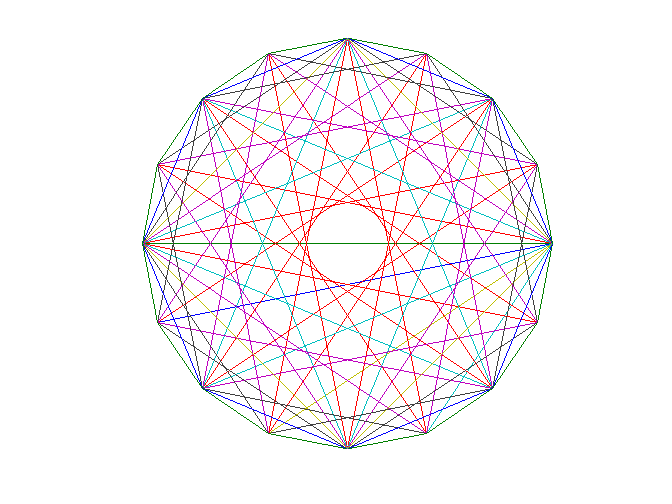
这是16阶傅里叶矩阵的一个图。像这样的图是本系列下一篇文章的主题。现在，请注意这是不具有16个节点的完整图。

情节(fft(眼睛(16)))轴相同的轴关

工具书类

史蒂夫·埃丁斯（Steve Eddins）在他的博客中大量撰写了关于FFT的文章。选择“类别更多”，然后单击“傅里叶变换”。< https://blogs.mathworks.com/steve>

James W.Cooley和John W.Tukey，“复傅里叶级数的机器计算算法”，数学。计算机。19: 297-301, 1965.< http://dx.doi.org/10.2307%2F2003354>

Matteo Frigo和Steven G.Johnson，“FFTW，西方最快的傅里叶变换”，< http://www.fftw.org>.

获取MATLAB代码

与MATLAB®R2014a一起发布