这是一个经典的难题。一对梯子靠在小巷的侧面，形成了一个偏斜的十字架。每个梯子都被支撑在一堵墙的底部，并靠在对面的墙上。如果一个梯子长30英尺，另外20英尺长，而它们越过地面10英尺的点，小巷有多宽？

内容

Eight variables

The lengths of the ladders are denoted by $a$ and $b$. The height of the crossing is $c$. The heights of the points where the ladders reach the walls are $x$ and $y$. The bases of the right triangles whose common height is the crossing are $u$ and $v$. Finally, the width of the alley is $w$. Here is the picture.

ladders_diagram('vars'）

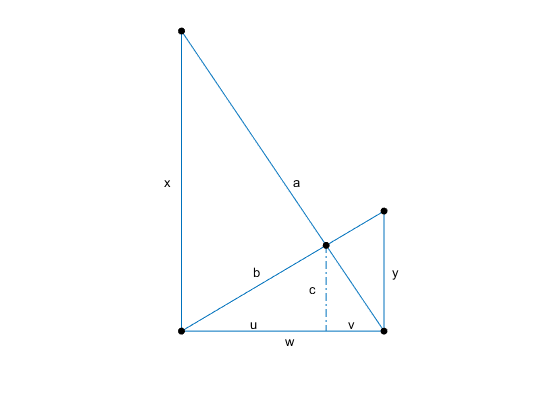
方程

这八个变量通过五个方程式连接。毕达哥拉斯定理提供了两个方程。

$$ a^2 = x^2 + w^2 $$

$$ b^2 = y^2 + w^2 $$

类似三角形的边之间的比率再提供两个。

$$ \ frac {x} {w} = \ frac {c} {v} $$

$$ \ frac {y} {w} = \ frac {c} {u} $$

The fifth equation is a simple linear relation that ties the two triangles together.

$$ w = u + v $$

涉及八个变量的五个方程式留下了三个自由度。原则上，我们可以指定任何三个变量并为其他五个变量求解。但这可能会或可能并不容易。我们将在下面的情况下有两种不同的情况。开幕段中提出的难题指定$ a $，$ b $和$ c $，并要求找到$ w $。这是不平凡的。另一方面，我们的图形应用程序由$ x $，$ y $和$ w $驱动。当这三个被鼠标点击固定时，其他五个立即跟随。

Harmonic mean

Combining the last three equations generates an elegant relation. This isn't a new equation; it's a consequence of the ones we already have.

$$ \frac{1}{c} = \frac{1}{x} + \frac{1}{y} $$

This says that the height of the crossing is one-half of theharmonic meanof the heights of the two ladders. The equation is a familiar one in光学，，，，where it is known as the薄镜头方程。It relates the location of an image to the object distance and focal length.

Smallest integer solution

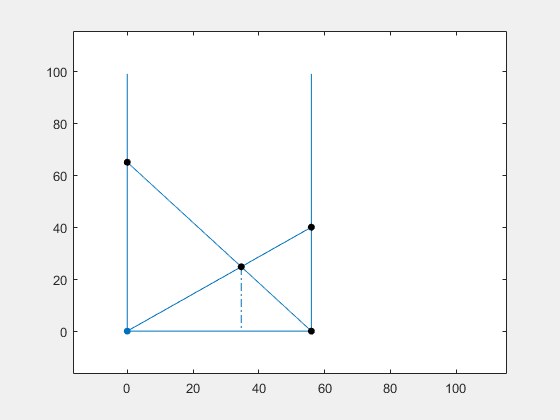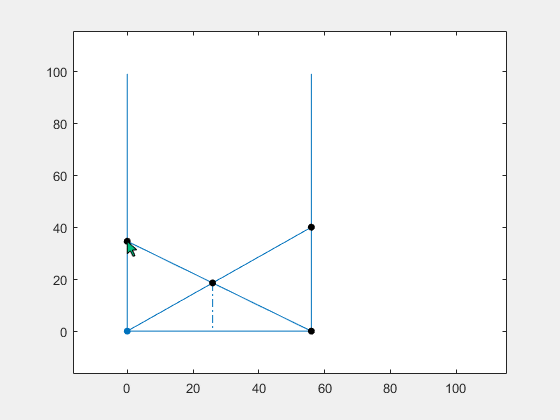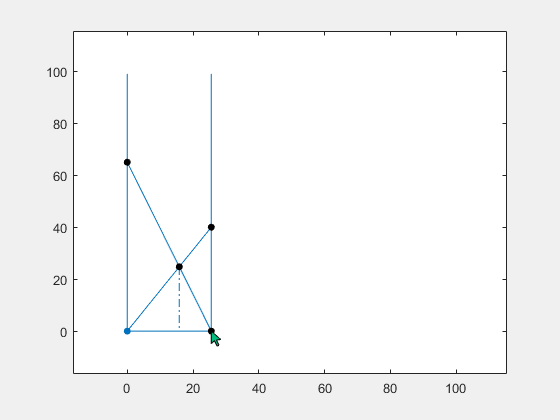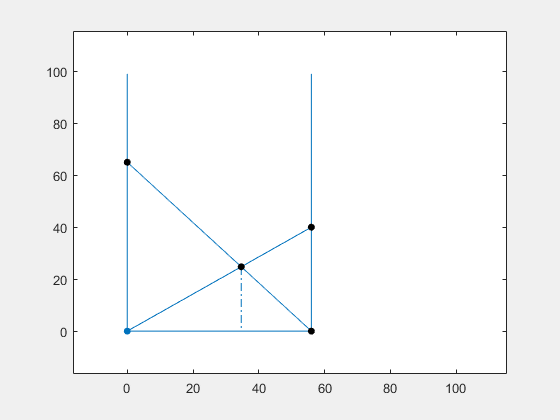
The following picture shows a solution of these equations where all eight variables have integer values. In fact, if we collect all eight variables into a vector $s$.

$$ s = [a, b, c, u, v, w, x, y] $$

并使用1纳米来测量溶液的“尺寸”。

$$ ||s||_1 = \sum_{i=1}^8 s_i $$

然后ITOT（“事实证明”）这是所有整数元素的最小解决方案。

ladders_diagram('vals'）

Puzzle

毕达哥拉斯和光学的组合提供了$ w $的单个非线性方程，以$ a $，$ b $和$ c $。

$ $ \压裂{1}{\√6 {^ 2 - w ^ 2}} + \压裂{1}{\sqrt{b^2 - w^2}}=\frac{1}{c} $$

使用一维MATLAB零查找器并不难fzerowith fixed values for一个，，，，b一个ndCto compute a solution of this equation.

一个= 30; b = 20; c = 10; F = @(w) 1./sqrt(a^2 - w.^2) + 1./sqrt(b^2 - w.^2) - 1/c w = fzero(F,c)

F = @(w)1./sqrt(a^2-w.^2)+1./sqrt(b^2-w.^2)-1/c w = 12.3119

So this is the answer to the puzzle. For the prescribed values of the lengths of the ladders and the height of the crossing point, the width of the alley has to be about12。3feet.

A graph ofF(w)in the vicinity of its zero shows whyfzero没有麻烦。

ezplot(F,[10,15]) set(gca,'xaxislocation'，，，，'起源'）line(w,0,“标记”，，，，'。'，，，，'markersize'，，，，24，，，，'color'，，，，'k'）

The gorilla in the room

很容易从数值上求解我们的单个非线性方程来计算$ W $，但是即使对于计算机代数系统，找到分析解决方案也是一个巨大的挑战。从历史上看，该方法集中在同等的四分之一多项式上。

Take $a = 40$, $b = 30$ and $c = 20$. Let

$$ z = w^2 $$

Multiply through by the expressions in the denominators to put everything on one level.

$$ 10\, \sqrt{400 - z} + 10\, \sqrt{900 - z} = \sqrt{400 - z}\, \sqrt{900 - z} $$

现在，双方都摆脱了右边的SQRT。然后重新排列术语并再次将所有内容保持平衡，以消除其余的SQRT。如果您小心，您最终将达到$ Z $中4度的多项式。

$$ z^4-2200 \，z^3 + 1630000 \，z^2-454000000 \，z + 385000000000000 = 0 $$

但是我们只有一半。我们仍然必须解决这个四重奏。原则上可以通过分析进行此操作，但让我们再次放弃代数并诉诸数字技术。

poly = [ 1, -2200, 1630000, -454000000, 38500000000]; z = roots(poly)

z = 1.0e+02 * 8.4877 + 0.5881i 8.4877 - 0.5881i 3.5087 + 0.0000i 1.5158 + 0.0000i

重复的平方已经产生了多余的根。我们可以从第四个收回$ w $。

w = sqrt（z（4））

W = 12.3119

It is reassuring to find the same width.

Ladders App

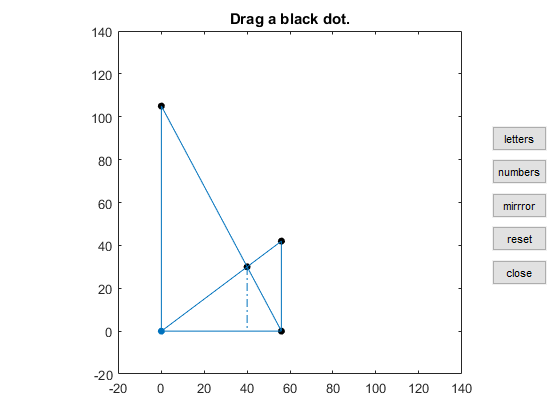
我在互动的图形体验中很有趣，您可以改变四个参数中的任何一个，并了解它如何影响其他参数。您可以更改梯子撞墙的点的高度，或更改小巷的宽度。您会发现，拖动这三个控制点中的任何一个仅影响其他数量的几个数量。

You will see more action when you vary the crossing point. This changes all of the values except the width. Of course, it is not physically realistic to expect to alter the lengths of the ladders by changing where they cross, but that would actually have to happen if they were constrained to meet the walls.

The complete program for this app is the subject for my blog in two weeks. The title is "Investigating the Classic Crossed Ladders Puzzle".This linkshould be good after March 14.

Acknowledgement

感谢Mathworks的Ned Gulley暗示这个经典的难题值得另一种外观。

Get the MATLAB code

与Matlab®R2016A一起出版