Cleve's Corner：数学和计算上的Clyver
Loren在Matlab的艺术上
史蒂夫在图像处理与matlab
Simulin金宝appk上的家伙
深度学习
开发人员区
Stuart的Matlab视频
在头条线后面
本周的文件交换选择
汉斯在某种程度上
赛车休息室
初创公司，加速器和企业家
Matlab社区
matlabユーザーコミュニティーQR算法计算特征值和奇异值
QR算法是世界上最成功的算法之一。我们可以使用动画GIF来说明算法的三个变型，一个用于计算非对称矩阵的特征值，一个用于对称矩阵，一个用于矩形矩阵的奇异值。在所有三种情况下，QR迭代本身在减少到紧凑的形式之前。所有转化都是使用Givens和Homeer转型的正交相似性。这些是数值稳定的，保持特征值，并保持任何对称性。
初始还原用途N-2住户相似在于一次在子目表下面介绍zeroes。结果称为一个Hessenberg矩阵（不要让拼写检查改变海森伯格矩阵。）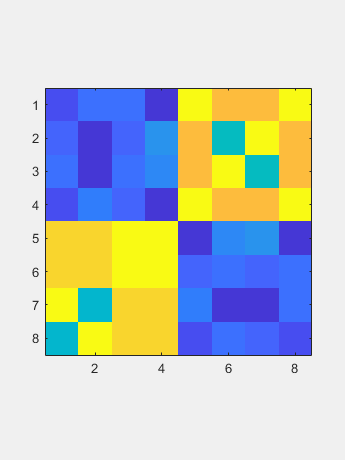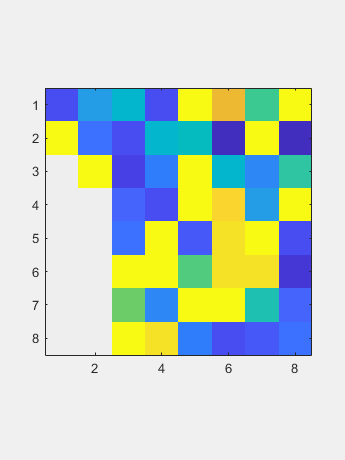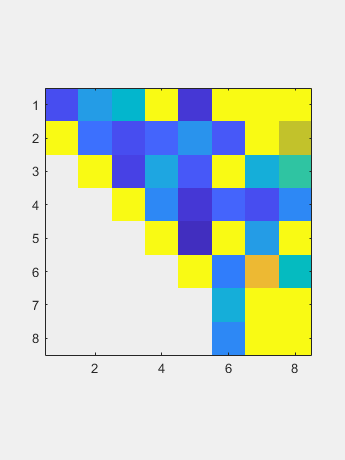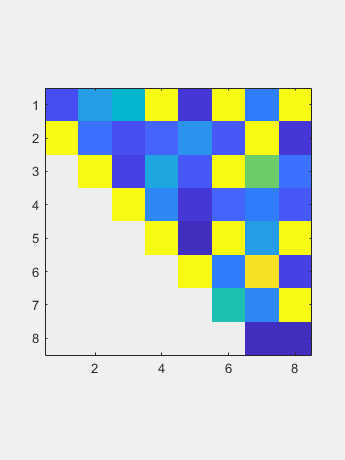
现在QR算法逐渐减少了大多数子间元素到圆形水平，因此它们可以设置为零。相应的对角元件是特征值。迭代计数显示在标题中。在最后一行中的对角线下方的元素是初始目标;它需要四个迭代。接下来的两行每次需要三个迭代。剩余的子通道只需要一个或两个迭代。
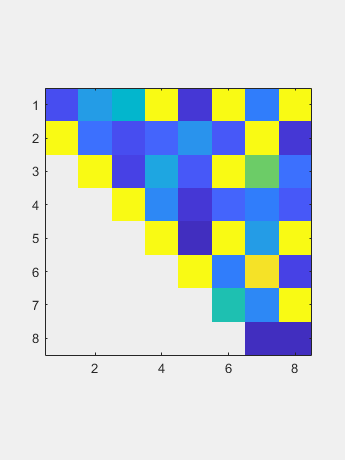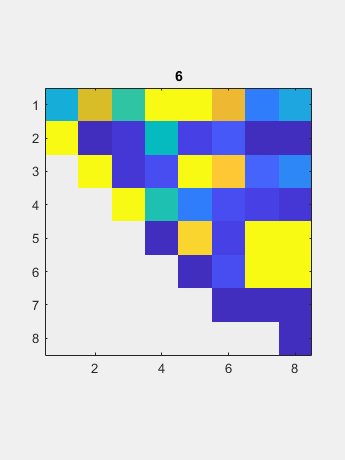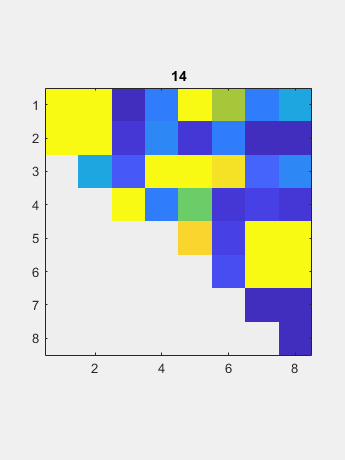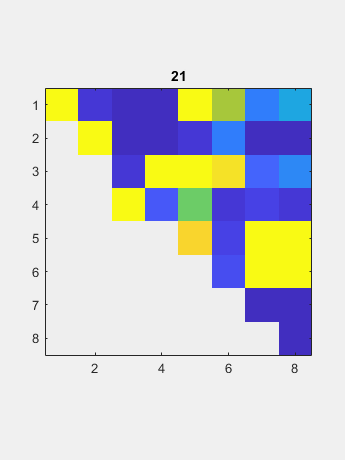这一切都是用真实算术完成的，尽管真实的非对称矩阵可能具有复杂的特征值。因此，最终矩阵可以在对角线上具有2×2凸起。该示例在行3和4中具有一个凸点。凸块的特征值是输入矩阵的复合缀合物对的特征值。所有其他对角线元素都是输入矩阵的真实值。
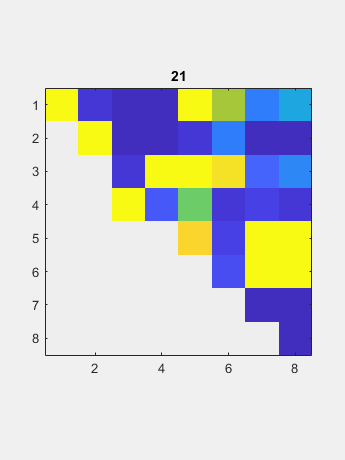计算的特征值是：
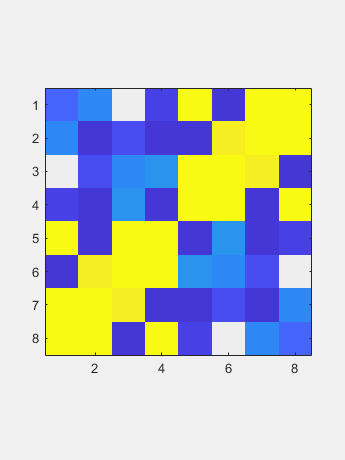通过对称，六个户主归零列的零点也为行。
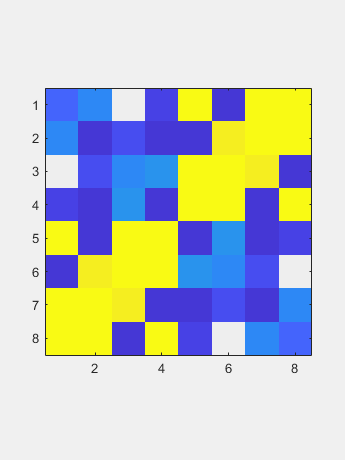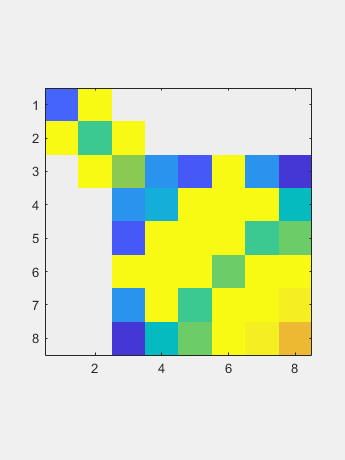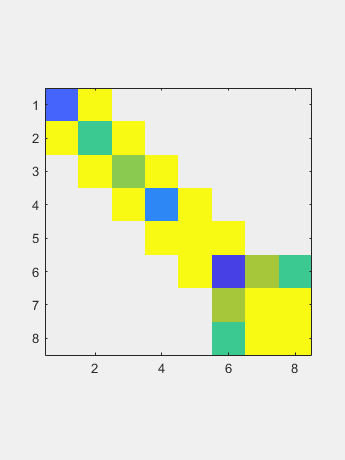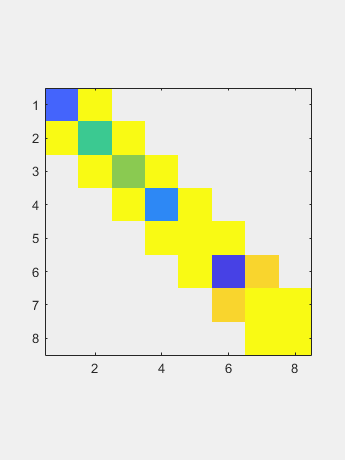现在QR迭代仅适用于两个向量，对角线和非对角线。
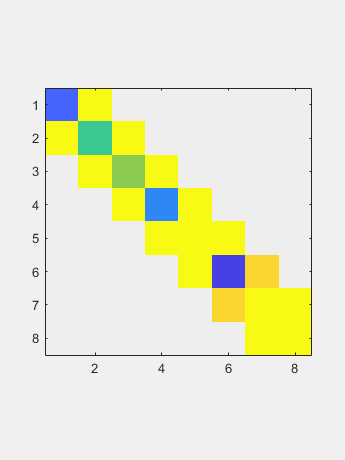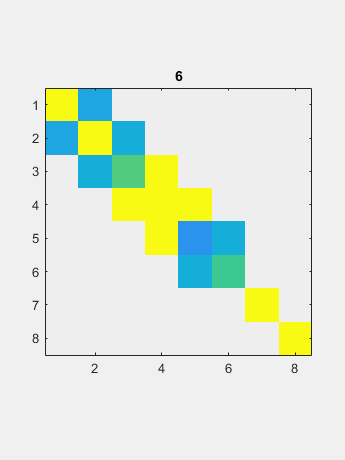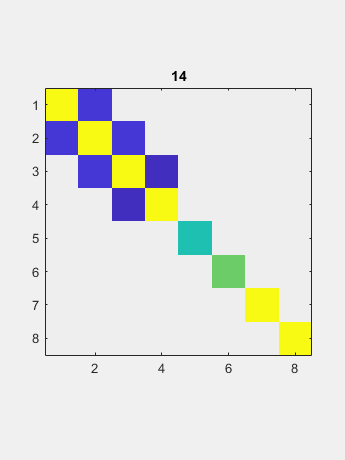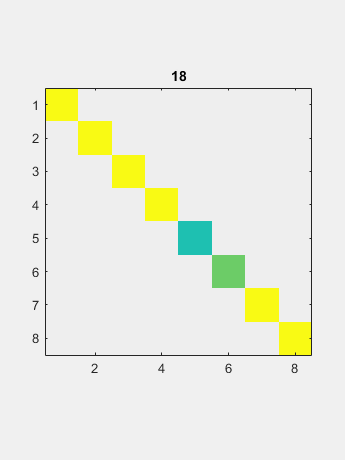极限是包含特征值的对角线。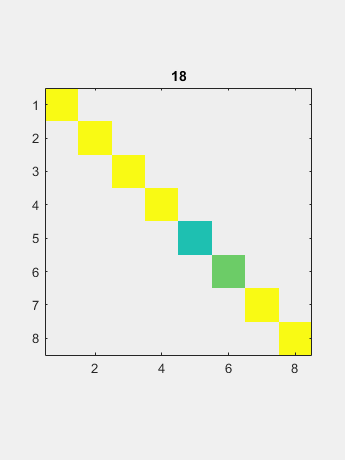
使用从左侧操作的家庭患者到零一列，然后将另一个家庭从右侧运行到零的大部分。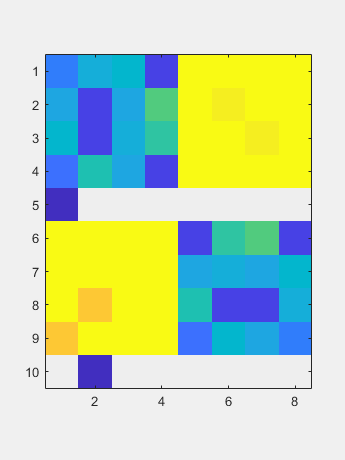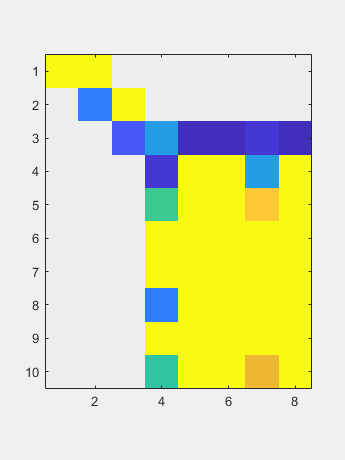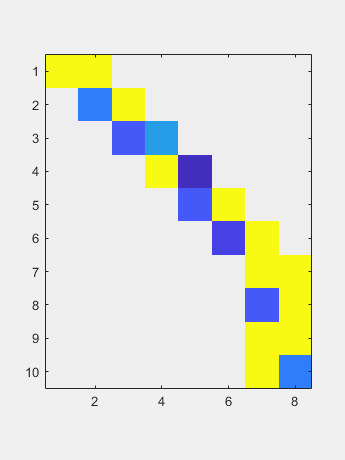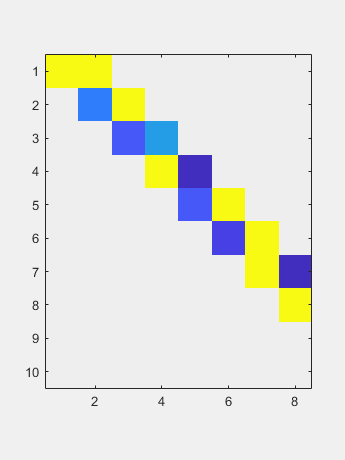
现在双面QR迭代减少了对角线的尺寸可忽略的尺寸。
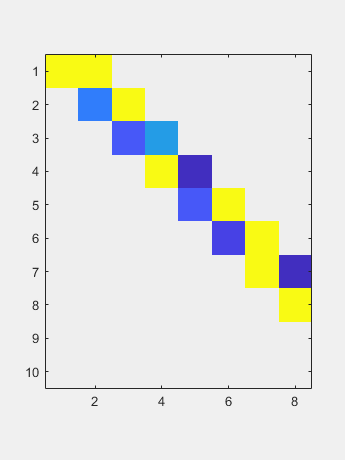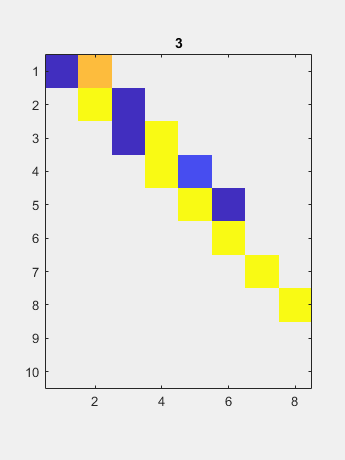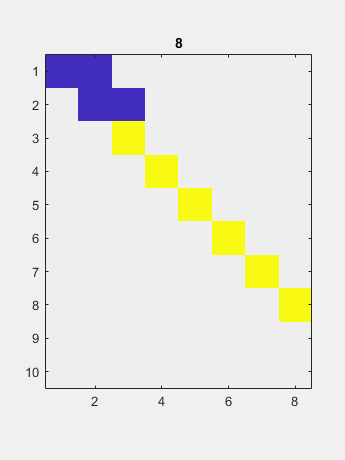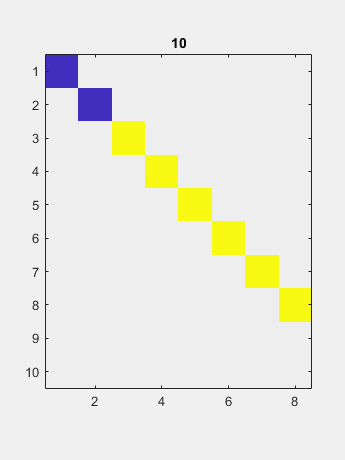得到的对角线包含奇异值。
内容
所有三种变体的起始矩阵基于翻转的rosser矩阵。a = pliplr（rosser）
A = 29 -49 -52 -8 407 -192 196 611 -44 -8 -43 -71 -192 113 899 196 52 8 49 61 196 899 113 -192 -23 59 44 8 611 196 -192 407 208 208 208 -599411 8 61 -71-8 208 208 411-594 49 -43 -52 -911 99 208 208 59 8 -8 -49 99 -911 208 208 -23 52 -44 29
非对称的特征值
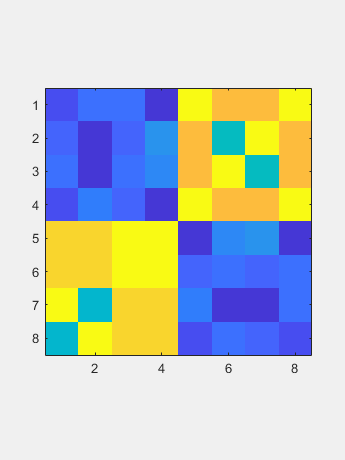
这是启动矩阵的静态图片。请注意，它不对称。
初始还原用途N-2住户相似在于一次在子目表下面介绍zeroes。结果称为一个Hessenberg矩阵（不要让拼写检查改变海森伯格矩阵。）
现在QR算法逐渐减少了大多数子间元素到圆形水平，因此它们可以设置为零。相应的对角元件是特征值。迭代计数显示在标题中。在最后一行中的对角线下方的元素是初始目标;它需要四个迭代。接下来的两行每次需要三个迭代。剩余的子通道只需要一个或两个迭代。
这一切都是用真实算术完成的，尽管真实的非对称矩阵可能具有复杂的特征值。因此，最终矩阵可以在对角线上具有2×2凸起。该示例在行3和4中具有一个凸点。凸块的特征值是输入矩阵的复合缀合物对的特征值。所有其他对角线元素都是输入矩阵的真实值。
计算的特征值是：-1010.9 1017.3 -14.529 + 903.74i -14.529 - 903.74i 206.9 -30.004 1.7094 5.614E-13
对称的特征值
一个对称矩阵是s =（a + a'）/ 2;FPRINTF（[REPMAT（'％7.1f'，1,8）'\ n']，s）
29.0 -11.5 307.5 8.0 -1157.5 -8.0 -17.5 -6.0 8.0 -17.5 499.0 -17.5 49.0 52.5 -201.5 655.0 160.5 8.0 -15.5 -6.0 52.5 8.0 511.0 -201.5 8.0 307.5 307.5 8.0 -201.5 511.08.0 52.5 -6.0 -15.5 8.0 160.5 655.0 -201.5 52.5 49.0 -17.5 0.0 -357.5 499.0 160.5 8.0 -6.0 -17.5 -8.0 -46.5 355.0 -357.5 8.0 307.5 -15.5 0.0 -46.5 29.0这是静态图片。（计算完成了矩阵的一半，但我们显示整个数组。）
通过对称，六个户主归零列的零点也为行。
现在QR迭代仅适用于两个向量，对角线和非对角线。
极限是包含特征值的对角线。
-1010.9 1017.4 -558.86 -481.89 -86.32 109.7 662.7 504.27
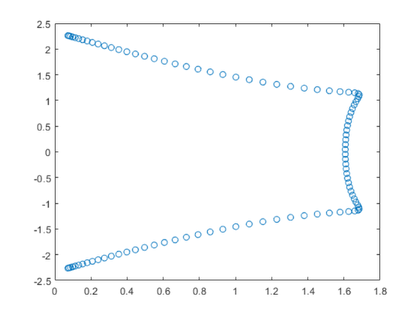
SVD.
通过插入几行的标识矩阵来使我们的测试矩阵矩形。我=眼睛（8,8）;a = [a（1：4，:);我（1，:);一个（5：8，:);我（2，:)]
A = 29 -49 -52 -8 407 -192 196 611 -44 -8 -43 -71 -192 113 899 196 52 8 49 61 196 899 113 -192 -23 59 44 8 611 196 -192 407 1 0 0 00 0 0 208 208 -599 411 8 61 -71 -8 208 208 411-599 44 49 -43-52 -911 99 208 208 59 8 -8 -49 99 -911 208 208 -23 52 -44 29 0 10 0 0 0 0 0
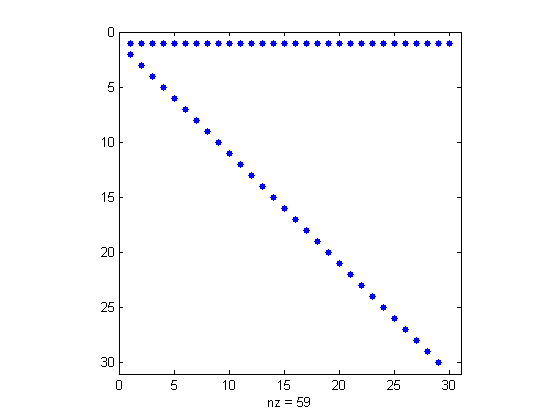
使用从左侧操作的家庭患者到零一列，然后将另一个家庭从右侧运行到零的大部分。
现在双面QR迭代减少了对角线的尺寸可忽略的尺寸。
得到的对角线包含奇异值。
0.44272 0.13184 1000 1000 1019.9 1020 1020 1020
软件
看Eigsvdgui.在MATLAB的数值计算或者克利夫的实验室。
|
注释
要发表评论，请点击这里登录您的MathWorks帐户或创建新的。