线性变换的秩是线性代数中的基本概念，矩阵因式分解是数值线性代数中的基本概念。吉尔斯特朗的线性代数2020愿景试图在线性代数入门课程早期介绍这些概念。

的CR矩阵分解提供了一个视图rref，即行简化阶梯形，作为一种揭示秩的矩阵分解。我讨论了CR在一个一对的的帖子10月。我现在要描述出租车因式分解，使用rref两次，以便以相同的方式处理行和列。

吉尔和我正在写一篇关于这些想法的综述论文，LU和CR的消除．这是当前草案的链接，LUCR_43.pdf．

内容

出租车

这是一个快速的描述出租车．

[C,W,B] = cab(A)返回C = A(:，cols)， B = A(rows，:)， and W = A(rows,cols)，因此

A = C*inv(W)*B

[C,W,B,cols,rows] = cab(A)也返回索引cols和rows。

所有的元素C，W而且B都是从输入矩阵中提取的一个本身;C是它的一些列，B它的一些行，和W集合的交点是C而且B．实际上,关口而且行这些都是因式分解计算。列指标来自行简化阶梯形，rref (A)，和转置后的行指标，rref(的)．

排名

一个矩阵的线性无关的列数等于线性无关的行数这一事实不是简单的，需要证明。这个数字是排名矩阵的，是非奇异点的大小W．

W是r乘r，其中rank(A) = r = length(cols) = length(rows)。

如果你试着去找C，W而且R与一个W那就太小了C *发票(W) * R会不会无法繁殖一个．如果W太大了，就会奇异。

排一个

如果一个排名第一，A = u*v'对于列向量u行向量v '．然后C是的倍数u，B是的倍数v ',W第一个非零元素在吗u或v．这里有一个例子，第一行故意为零。

A = (0:3)'*(4:6)

A = 0 0 0 4 5 6 8 10 12 12 15 18

格式紧凑的[C,W,B] =出租车(A)

C = 0 4 8 12 w = 4 b = 4 5 6

二阶

在这个例子中，即使是随意的检查也会显示出等级。请注意,一个是长方形的。

A =重塑(1:24,4,6)'

A = 12 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

[C,W,B,cols,rows] = cab(A)

C = 1 2 5 6 9 10 13 14 17 18 21 22 W = 1 2 5 6 B = 1 2 3 4 5 6 7 8 cols = 1 2 rows = 1 22

Rank = length(cols)

Rank = 2

满秩

如果A是平方且非奇异的，则C = B = W = A。

例如,

A = pascal(3)

A = 1 1 1 1 2 3 1 3 6

[C,W,B] =出租车(A)

C = 1 1 1 1 2 3 1 3 6 w = 1 1 1 1 2 3 1 3 6 b = 1 1 1 1 2 3 1 3 6

富兰克林魔方

富兰克林半幻方形是本杰明·富兰克林在1752年发明的。富兰克林给他的一位同事的一封信包含在下面引用的富兰克林论文中。

富兰克林方阵的所有行和列都有所需的神奇和，但对角线没有，所以矩阵并不是完全神奇的。然而，许多其他有趣的子矩阵是神奇的，包括弯曲的对角线和围绕中心对称排列的任何八个元素。

这个8 × 8矩阵的秩是多少?

富兰克林(8)

A = 52 61 4 13 20 29 36 45 14 3 62 51 46 35 30 19 53 60 5 12 21 28 37 44 11 6 59 54 43 38 27 22 55 58 7 10 23 26 39 42 9 8 57 56 41 40 25 24 50 63 2 15 18 31 34 47 16 1 64 49 48 33 32 17

很难把富兰克林平方看做一个线性变换，但是出租车仍然可以计算它的秩。

[C,W,B] =出租车(A)

C = 52 61 4 14 3 62 53 60 5 11 6 59 55 58 7 9 8 57 50 63 2 16 1 64 w = 52 61 4 14 3 62 53 60 5 b = 52 61 4 13 20 29 36 45 14 3 62 51 46 30 19 53 60 5 12 21 28 37 44

所以秩只有3。

计算C *发票(W) * B引入一些舍入错误。

test = C*inv(W)*B;显示器(“测试”）

测试= 52.00 61.00 4.00 13.00 20.00 29.00 36.00 45.00 14.00 3.00 62.00 51.00 46.00 35.00 30.00 19.00 53.00 60.00 5.00 12.00 21.00 28.00 37.00 44.00 11.00 6.00 59.00 54.00 43.00 38.00 27.00 22.00 55.00 58.00 7.00 10.00 23.00 26.00 39.00 42.00 9.00 8.00 57.00 56.00 41.00 40.00 25.00 24.00 50.00 63.00 2.00 15.00 18.00 31.00 34.00 47.00 16.00 1.00 64.00 49.00 48.00 33.00 32.00 17.00

舍入测验到最接近的整数，就能精确地再现富兰克林的魔方。

反斜杠和正斜杠

用(C/W)*B或C*(W\B)计算C*inv(W)*B通常更准确。如果A有整数元素，您可以尝试圆(C/W*B)或圆(C*(W\B))。

这个5乘5矩阵是故意构造的，因此它的秩缺陷并不明显。

A =画廊(5)

A = -9 11 -21 63 -252 70 -69 141 -421 1684 -575 575 -1149 3451 -13801 3891 -3891 7782 -23345 93365 1024 -1024 2048 -6144 24572

[C,W,B] =出租车(A)

C = -9 11 -21 63 70 -69 141 -421 -575 575 -1149 3451 3891 -3891 7782 -23345 1024 -1024 2048 -6144 w = -9 11 -21 63 70 -69 141 -421 575 575 -1149 3451 3891 -3891 7782 -23345 b = -9 11 -21 63 -252 70 -69 141 -421 1684 -575 575 -1149 3451 -13801 3891 -3891 7782 -23345 93365

rank = size(W,1)

排名= 4

在这个例子中，W有轻微的病态。

kappa = cond(W)

Kappa = 2.4301e+04

有三种方法来重建一个．

inw = C*inv(W)*B;背= (C/W) * B;前= C * (W\B);

的条件影响反演后的相对误差W，而反斜杠和正斜杠几乎要准确5个数量级，

格式短erelerr = [norm(A-invw) norm(A-fore) norm(A-back)]/norm(A)

Relerr = 2.1266e-13 4.7760e-18 3.7217e-17

这三个整数中的任何一个四舍五入都会得到结果一个完全正确。

A = round(C*inv(W)*B)

A = -9 11 -21 63 -252 70 -69 141 -421 1684 -575 575 -1149 3451 -13801 3891 -3891 7782 -23345 93365 1024 -1024 2048 -6144 24572

Gauss-Jordan

计算的算法rref是高斯-乔丹消去法，它在数值分析界有一个可疑的名声。在听了我试图描述算法的臭名昭著之后，Gil在的介绍段落中写道我们的调查高斯-乔丹算法“昂贵且在数值上很危险”。

“昂贵”的部分很容易解释。的计算rref在一个列中，在主元的上面和下面都引入零，而高斯消去只在主元下面引入零。工作量更少。我们可以用一个融合的乘法-加法指令(FMA)来衡量计算复杂度，该指令将两个浮点值相乘，然后在一次操作中向结果添加第三个值。对于一个大型的n × n系统，高斯-乔丹算法需要大约(1/2)n^3 fma，而高斯消去算法只需要较少的(1/3)n^3 fma。

然而，我们并不打算这样做CR而且出租车用于大矩阵。对于我们的目的，即使使用两次Gauss-Jordan也不昂贵。

高斯-乔丹声名中“数字上的危险”的部分更为微妙。它来自于解一个线性系统A*x = b通过计算rref增广矩阵，[b]．另一方面，高斯消去法可以找到三角因子l而且U然后计算x通过反向替换。我们可以说高斯消去是部分而Gauss-Jordan是完整的消除。Jim Wilkinson和Gwen Peters在1975年的论文中对这两种方法进行了比较。高斯消去几乎总是计算附近系统的解，但对于增广矩阵上的高斯- jordan却不能这样说。

但是，我们没有使用任何一种消元法来计算出租车因素;rref只是选择索引。的矩阵C，W而且B从出租车(A)的子矩阵一个．他们当然是准确的。有两个潜在的数字困难W可能是条件不好，也可能是尺寸不对。

条件

如果一个条件不好吗?然后W必须继承这种条件。这里有一个例子。开始

N = 12;U = eye(n,n) - triu(ones(n,n)，1)

U = 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1

U条件很差。电导率(U, 1)而且电导率(U,正)都等于n * 2 ^ (n - 1)．

让

A = u '* u

= 1 1 1 1 1 1 1 1 1 1 1 1 1 2 0 0 0 0 0 0 0 0 0 0 1 0 3 1 1 1 1 1 1 1 1 1 1 0 1 4 2 2 2 2 2 2 2 2 1 0 1 2 5 3 3 3 3 3 3 3 1 6 0 1 2 3 4 4 4 4 4 7 4 1 0 1 2 3 4 5 5 5 5 5 1 0 1 2 3 4 5 6 8 6 6 6 1 0 1 2 3 4 5 6 7 9 7 7 10 1 0 1 2 3 4 5 6 7 8 8 1 0 1 2 3 4 5 6 7 8 9 11 1 0 1 2 3 4 5 6 7 8 9 12

一个是对称的，正定的，满秩的。的行列式一个等于1。我看不出一个简洁的公式气孔导度(A)但我知道它长得像4 ^ n．

自一个是满秩，其A = C*inv(W)*B因式分解必须A = A*inv(A)*A．

[C,W,B] =驾驶室(A);test = [isequal(C,A) isequal(W,A) isequal(B,A)]

Test = 1×3逻辑阵列1 1 1

W条件很差。发票(W)具有较大的元素。

Winv = inv(W)

Winv =列1到6 87384 699051 349526 174764 1398102 43696 699051 349526 174763 87382 43692 21848 349526 174763 87382 43691 21846 10924 174764 87382 43691 21846 10923 5462 87384 43692 21846 10923 5462 2731 43696 21848 10924 5462 2731 1366 21856 10928 5464 2732 1366 683 10944 5472 2736 1368 684 342 5504 2752 1376 688 344 172 2816 1408 704 352 176 88 1536 768 384 192 96 48 1024 512 256 128 64 32列7到12 21856 10944 5504 2816 1536 1024 10928 5472 2752 1408 768 512 5464 27361376 704 384 256 2732 1368 688 352 192 128 1366 684 344 176 96 64 683 342 172 88 48 32 342 171 86 44 24 16 171 86 43 22 128 86 43 22 11 64 24 12 6 32 1 16 84 2 11 1

logWinv = floor(log2(Winv))

logWinv = 20 19 18 17 16 15 14 13 12 11 10 10 19 18 17 16 15 14 13 12 11 10 9 9 18 17 16 15 14 13 12 11 10 9 8 8 17 16 15 14 13 12 11 10 9 8 7 7 16 15 14 13 12 11 10 9 8 7 6 6 15 14 13 12 11 10 9 8 7 6 5 5 14 13 12 11 10 9 8 7 6 5 4 4 13 12 11 10 9 8 7 6 5 4 3 3 12 11 10 9 8 7 6 5 4 3 2 2 11 10 9 8 7 10 6 5 4 3 2 1 1 9 8 7 6 5 4 3 2 1 1 0 10 9 8 7 6 5 4 3 2 1 0 0

沿着对角线logWinv从(n, n)来(1,1)．

Winv(1,1) > 4^(n-2)

Ans =逻辑1

是一个接近一个低秩矩阵?答案是肯定的，但低秩近似来自SVD。

CAB vs SVD

的圣言会是揭示最终等级的因数分解，但它实际上并不试图计算等级。

[U,S,V] = svd(A)

计算一个完整的奇异值和向量集合，就像矩阵具有全秩一样。奇异值，s = diag(s)，按降序索引，

S(1) >=…>= s(r) >= s(r+1)…

您可以将奇异值与公差进行比较，以获得近似秩和因数分解。

有效秩的选择是由Eckart-Young-Mirsky定理:如果基于“增大化现实”技术是通过选择秩来近似的吗r，

Ar = U(:，1:r)*S(1:r,1:r)*V(:，1:r)'

误差的范数以省略的第一项为界，

范数(A - Ar,2) <= s(r+1)

如果奇异值迅速减小，则只需几个项即可获得精确的低秩近似。

另一方面，出租车从矩阵本身的列和行中选择基底。没有Eckert-Young定理CR或出租车分解。

我们打算CR而且出租车在课堂上用在小矩阵上，通常是整数项。我们将让SVD和随机矩阵分解处理大的东西。

参考文献

本杰明·富兰克林,本杰明·富兰克林文集，卷44,1750-53，给彼得·科林森。(美国哲学学会和耶鲁大学)第392页。https://franklinpapers.org/framedVolumes.jsp?vol=4&page=392a．

G. Peters和J. H. Wilkinson，“关于高斯-乔丹消去与旋转的稳定性”，ACM通讯18, 1975，第20-24页。https://dl.acm.org/doi/10.1145/360569.360653，另载于http://www.stat.uchicago.edu/~lekheng/courses/302/gauss-jordan2.pdf

附言

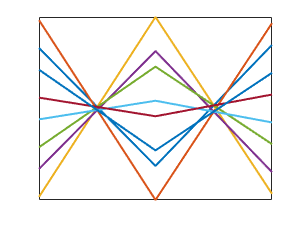
本·富兰克林也可以为今天的帖子提供图片。

A =富兰克林(8);[~，~，B] =驾驶室(A);情节(B)

获取MATLAB代码

发布与MATLAB®R2021a