算术结合律-没那么快
算术是结合的,对吧?在纸和铅笔的世界里,你可以精确地计算,这是正确的。然而,在计算世界中,由于使用的是有限精度的数据类型,实数不能总是精确地表示,结果是,你不能依赖算术来表现你在小学学到的方式。
内容
让我们做一些数学
假设我想检查以下内容:
${2} = 2/根号{2}$$
我可以用分析来做这个符号数学工具箱.
symsqrt2 =√符号(2));symsqrt2 - 2/symsqrt2 . shouldBeZero = symsqrt2 - 2/
shouldBeZero = 0
现在让我们用数字来做同样的计算。
mightBeZero =根号2 - 2/根号2
mightBeZero = 2.2204 e-16
这里所发生的是,我们看到了浮点数及其计算精度的影响。我在一个之前的帖子也
让我们试试另一个例子
现在让我们尝试一些不同的东西。首先,我们来看看每股收益为%根号{2}%。这应该是最小的(大小上的)浮点数,当加到%根号{2}%时,产生的数字与%根号{2}%不同。
sqrt2eps =每股收益(sqrt (2))
sqrt2eps = 2.2204 e-16
接下来,我们想要一个比这个大小更小的数字。我用它的一半值。
halfsqrt2eps = sqrt2eps / 2
halfsqrt2eps = 1.1102 e-16
现在让我们用符号和数字来计算下面的表达式。
$expr1 = sqrt{2} - sqrt{2} + halfsqrt2eps
$$expr2 = (\sqrt{2} - \sqrt{2}) + halfsqrt2eps$$
$expr3 = (- sqrt{2} + halfsqrt2eps)$ expr3 = (- sqrt{2} + halfsqrt2eps
首先我们象征性地做一下。
expr2 = (symsqrt2 -symsqrt2) + sym(sqrt2eps)/2 expr3 = sym(symsqrt2 + sym(sqrt2eps)/2) double(Expr1)
Expr1 = 1/9007199254740992 expr2 = 1/9007199254740992 expr3 = 1/9007199254740992
符号结果都是相同的,返回值的一半每股收益.
现在我们用数字来计算同样的表达式。
Expr1 =√(2)-√(2)+ halfsqrt2eps expr2 =√(2)-√(2)+ halfsqrt2eps expr3 =√(2)+(-√(2)+ halfsqrt2eps
Expr1 = 1.1102e-16 expr2 = 1.1102e-16 expr3 = 2.2204e-16
这是怎么回事?如前所述,这个示例说明了浮点算术不像符号算术那样具有关联性。对此感到不安是有理由的。但它值得理解。偶尔重写一次计算可能是值得的,特别是当你试图计算两个大数之间很小的差的时候。
你是否重写了表达以获得更好的准确性?
您是否发现自己处于这样一种情况,需要重写如何计算数值结果(如这里,通过不同的分组),以确保得到一个更准确的解决方案。让我知道这件事在这里.














 克利夫角:克利夫·莫尔谈数学和计算机
克利夫角:克利夫·莫尔谈数学和计算机 罗兰关于MATLAB的艺术
罗兰关于MATLAB的艺术 用MATLAB进行图像处理
用MATLAB进行图像处理 人在仿真软件金宝app
人在仿真软件金宝app 深度学习
深度学习 开发区域
开发区域 斯图尔特的MATLAB视频
斯图尔特的MATLAB视频 在标题后面
在标题后面 本周文件交换精选
本周文件交换精选 汉斯在物联网
汉斯在物联网 学生休息室
学生休息室 初创企业、加速器和企业家
初创企业、加速器和企业家 MATLAB社区
MATLAB社区 MATLABユーザーコミュニティー
MATLABユーザーコミュニティー

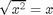

评论
要留下评论,请点击在这里登录到您的MathWorks帐户或创建一个新帐户。