今天，我想欢迎Josh Meyer成为本周的客座博主。Josh在MathWorks的文档团队工作，他在那里编写和维护一些MATLAB数学文档。在这篇文章中，Josh就如何选择使用哪种ODE解算器提供了一些建议。交给你，Josh。。。

内容

初始价值问题

Matlab中有7个常微分方程初始价值问题求解器：

（注意ode15i因为它解决了它自己的一类初值问题：形式为$f（t，y，y'）=0$的完全隐式常微分方程

要在求解器中进行选择，首先必须了解为什么对于给定的问题，一个求解器可能比另一个更好。

Matlab中的ODE求解器都在表格的初始价值问题上工作，

$$y' = f \left(t,y \right)$$

其中$y' = dy/dt$。还有一种更普遍的形式，

$ M(t,y) y' = f \left(t,y \right)$

其中$M（t，y）$被称为质量矩阵．

从初始条件$y_0$开始，再加上一段需要得到答案的时间$(t_0,t_f)$，根据求解算法，利用前面步骤的结果迭代求解。在这样的第一步，初始条件提供了必要的信息，允许进行集成。最后的结果是ODE求解器返回一个时间步长向量$t_0,t_1，…，t_f$以及每一步$y_0,y_1，…，y_f$对应的解。

理论上，由于微积分基本定理提供的微分方程和积分之间的联系，这种数值求解技术是可能的：

$ $ y (t + h) = y (t) + \ int_t ^ {t + h} f \离开(年代,y (s) \右)ds $ $

计算$y(t+h)$的问题变成了如何近似右边的积分的问题。这就是不同求解器的用武之地。每个不同的求解器使用不同的数值技术计算积分，每个求解器在效率和精度之间进行权衡。

例子：欧拉方法

欧拉方法是一个简单的ODE求解器，但它提供了一个例子，在ODE求解器算法的效率和精度之间的权衡。假设你想解

$ f(t,y) = 2t$

在时间跨越$ [0,3] $使用初始条件$ y_0 = 0 $。使用euler方法的每个步骤

$$\begin{array}{cl}y{n+1}&=y{n+hf\left（t{n，y{n\right）\\t{n+1}&=t{n+h\end{array}$$

使用$h=1$，解决方案只需要三个步骤:

$$ \ begin {array} {cl} y_1＆= y_0 + f \ left（t_0，y_0 \右）= 0 \\ y_2＆= y_1 + f \ left（t_1，y_1 \ ole）= 2 \\ y_3＆= y_2 + f \ left（t_2，y_2 \右）= 6 \ end {array} $$

..．但它准确吗?

不完全是。这个方程的精确解是

$ $ y (t) = t ^ 2 $ $

减小步长$h$可以稍微提高答案的准确性，但也需要更多的步骤来实现解决方案。要了解这一点，下面的代码使用Euler方法解决了此问题，并将答案与解析解进行比较，得出几个不同的$h$值。

清晰，clc h=1；tspan=[03]；f=@（t，y）2*t；dydt（1）=0；t（1）=0；y=@（t）t.^2；x=linspace（0，tspan（end））；图形图（x，y（x））xlabel(“t”), ylabel ('y（t）')举行在而H> 0.1为k = 2：Tspan（末端）/ h + 1 dydt（k）= dydt（k-1）+ h * f（t（k-1），dydt（k-1））;t（k）= t（k-1）+ h;结束情节(t, dydt“o”）H = H / 2;结束传奇（精确解的，“h = 1”，“h = 0.5”，'h = 0.25'，“h = 0.125”，..．“位置”，“西北”)头衔(“使用具有多个步长的欧拉方法求解y'=2t”）

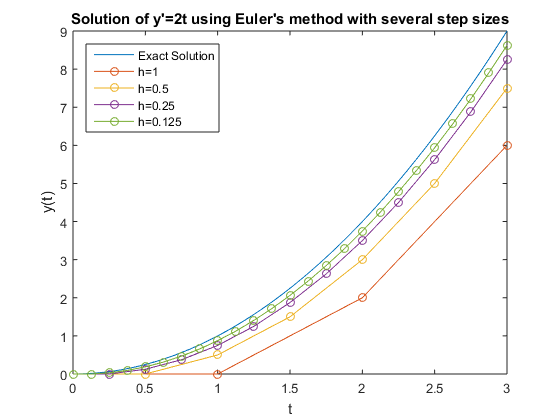
欧拉法的改进

使用越来越小的步长并不是一个好主意，因为算法会降低效率。对于任何合理的问题，这样的解决方法将是非常缓慢的。此外，欧拉法也存在一些固有的问题。因为$y$的斜率只在每个区间的开始处计算一次，所以这个解算器只对常数函数给出精确的答案。也没有办法估计误差，因此求解器需要使用固定的步长。

因此，改进欧拉方法的一种方法是在每一步中更频繁地计算$y'$。这提供了中间斜率，可以更好地了解函数在每个区间内的运行情况，从而使求解器能够为高阶问题提供精确的答案。例如，如果你在欧拉方法中加入对每个区间中间的斜率的评估，那么结果就叫做中点规则，对线性函数进行精确积分:

数组$ $ \开始{}{cl} s_1 & = f (t_n推出)\ \ s_2 & = f \离开(t_n + \压裂{h}{2},推出+ \压裂{h} {2} s_1 \) \ \ y_ {n + 1} & =最大+ hs_2 \ \ t_ {n + 1}识别& = t_n + h \{数组}$ $

如果在每个区间求四次斜率，就得到经典龙格库塔算法(或称。RK4)，这是数值算法。这个算法产生了三次函数的精确积分(如果$f$只是一个关于$t$的函数，那么$s_2=s_3$，这和辛普森的规则交):

数组$ $ \开始{}{cl} s_1 & = f (t_n推出)\ \ s_2 & = f \离开(t_n + \压裂{h}{2},推出+ \压裂{h} {2} s_1 \) \ \ s_3 & = f \离开(t_n + \压裂{h}{2},推出+ \压裂{h} {2} s_2 \) \ \ s_4 & = f \离开(t_n + h,推出+ hs_3 \) \ \ y_ {n + 1} & =最大+ \压裂{h}{6} \离开(s_1 + 2 s_2 + 2 s_3 + s_4 \) \ \ t_ {n + 1}识别& = t_n + h \{数组}$ $

Runge-Kutta算法都是单步求解器，因为每个步骤仅取决于前一步骤的结果。数值，ode23，ode23s，ode23t,ode23tb所有算法都采用单步算法。多步算法，如ode113和ode15s，使用几个过去的步骤的结果。

像MATLAB中的复杂的颂歌求解器也估计每个步骤中的错误，以确定下一步尺寸应该有多大。这是通过上述固定步长的另一个改进，因为每个步骤执行更多工作的求解器，能够通过采取不同尺寸的步骤来补偿。用于确定步长的误差估计通常通过比较两种不同方法的结果来获得。Matlab的颂歌遵循一个命名约定，揭示了关于他们使用的方法的信息。数值比较四阶龙格-库塔法和五阶龙格-库塔法的结果，确定误差。同样的,ode23使用了二阶和三阶龙格-库塔比较。所以，一般来说，数字越小odeNN，Looser求解器的错误容忍度是。

那么，这就不足为奇了数值得到了之前用欧拉法求解的方程的一个非常精确的答案。数值是Matlab的通用颂歌求解器，它是您应该为大多数问题使用的第一个解决者。

Y = @(t) t.²;x = linspace (0, 3);图绘制(x, y (x))包含(“t”), ylabel ('y（t）')举行在[t,y] = ode45(@(t,y) 2*t， [0 3]， 0);情节(t y“哦”)包含(“t”), ylabel ('y（t）')头衔('解y' =2t使用ode45'）

僵硬的微分方程

对于一些ODE问题，求解器所采取的步长被强迫降至一个不合理的小水平，与积分区间相比，即使在求解曲线是平滑的区域。这些步长可能非常小，以至于穿越一个短时间间隔可能需要数百万次计算。这可能导致求解器在集成中失败，但即使它成功了，也需要很长时间才能做到。

在ODE求解器中导致这种行为的方程被称为僵硬的．这是一个对等方程顽固而不容易被数值技术进行评估的事实。僵硬的问题姿势是明确的求解器（如数值)解决问题的速度慢得站不住脚。这就是为什么数值与一起被分类为非IFF解算器ode23和ode113．这些求解者都在努力地对僵硬的方程进行积分。

方程刚度需要一个精确的定义，因为有几个因素导致它。刚度是由特定方程、ODE求解器、初始条件和求解器所使用的误差公差的组合而产生的。以下关于刚度的陈述，归因于Lambert[6]，在许多刚性ode的例子中得到了证明，但也存在反例，因此它们不是刚度的真定义:

这些声明的一个共同主题是，刚度可能是由问题中某个地方的伸缩差异造成的。这种尺度上的差异(例如，如果雅可比矩阵$J =偏f_n/偏y_i$有很大比例的负特征值)限制了求解器在执行积分时所能采取的步长。为了保持解决方案中的容错性或稳定性，微小的步长是必要的。

例如，描述化学反应的方程式经常显示刚性，因为溶液的组分通常在截然不同的时间尺度上发生变化（同时发生的反应既非常缓慢又非常快速）。

然而，有专门设计用于处理刚性ode的求解器。为刚性问题设计的求解器通常每一步做更多的工作，与非刚性求解器相比，它们能够采取更大的步骤，并享有更好的数值稳定性。刚性求解器是隐式的，因为$y$的计算需要使用线性代数来求解线性方程组。随着积分的进行，雅可比矩阵被用来估计ODE的局部行为，因此提供解析雅可比矩阵可以提高MATLAB的刚性ODE求解器的性能。

这只是对僵硬的奇妙治疗，因为它是一个复杂的话题。看常微分方程:刚度以获得更深入的了解。

总之，MATLAB中的非刚性解算器包括：

僵硬的解算器（当数值速度慢）：

应该注意的是，非刚性求解者会这样做工作在刚性问题上，这只是因为它们异常缓慢。类似地，为刚性问题设计的解算器可以处理非刚性问题，但由于它们每一步都要做更多的工作，因此在不需要额外工作的情况下，它们的效率低于非刚性问题的解算器。因此方程刚性是一个解算器效率的问题，目标是在解决方案的精度和解算器在每个步骤中完成的工作之间取得正确的平衡。

解决的建议

以下建议改编自Matlab数学文件：

为non问题:

为僵硬的问题（在哪里数值速度慢）：

以下是捕获基本建议的图形。在大多数情况下，求解件的唯一选择您需要制作ode15s而不是数值．

例1:阻尼摆

阻尼摆的运动方程是，

$$\ddot{\theta}=-\frac{b}{m}\dot{\theta}-\frac{mg}{L\left（m-2b\right）}\sin\theta$$

其中$ g $是引力常数，鲍勃的质量为鲍勃的质量，$ l $的字符串的长度，$ b $是阻尼系数。目标是为了获得$ \ theta $，摆锤偏离垂直的角度，以及$ \ theta'$，角度变化的速率。

一些自然的初始条件是$\theta_0 = pi/4$和$\theta '_0 = 0$，这表示你在放手前将钟摆抬高到45度角，并且它没有初始角速度。由于阻尼系数，你会认为钟摆会慢慢失去动量，回到静止状态。

文件pendulumODE.m作为一阶ODES的耦合系统重新重新装饰问题：

数组$ $ \开始{}{cl} y_1’& = y_2 \ \ y_2 ' & = - \压裂{b} {m} y_2 - \压裂{mg} {L (m-2b)}罪(y_1) \{数组}$ $

然后解决使用数值，ode15s，ode23,ode113．绘制$ 金宝搏官方网站y_1 = \ theta $的解决方案，文件返回每个求解器的统计数据。显示执行时间时始终如此，“显示的定时可以变化”。

函数opts = odeset(“统计数据”，“上”）;tspan = [025];Y0 = [PI / 4,0];disp ('')，disp(的统计数值:)tic，[t1，y1]=ode45（@pendode，tspan，y0，opts）；toc显示('')，disp(“ode15s统计:) tic， [t2,y2] = ode15s(@pendode, tspan, y0, opts);toc disp ('')，disp('ODE23的统计数据：') tic， [t3,y3] = ode23(@pendode, tspan, y0, opts);toc disp ('')，disp(“ode113统计:)tic，[t4，y4]=ode113（@pendode，tspan，y0，opts）；toc地物子地块（2,2,1），绘图（t1，y1（：，1），“o”)，xlim（[0 25]），标题(“ode45”）子图（2,2,2），绘图（T2，Y2（：，1），“o”)，xlim（[0 25]），标题(“ode15s”)次要情节(2、2、3),情节(t3, y3 (: 1),“o”)，xlim（[0 25]），标题(“ode23”)次要情节(2、2、4),情节(t4, y4 (: 1),“o”)，xlim（[0 25]），标题(“ode113”）函数y = 0,y = 0;% m / s ^ 2m = 1;％鲍勃L=2；%摆锤长度（米）B = 0.2;%阻尼系数dy2dt2=[y（2）；-b/m*y（2）-g/L*sin（y（1））；结束结束

pendulumODE

ode45的Stats: 75个成功的步骤0个失败的尝试451个函数计算运行时间为0.011970秒。ode15s的统计:183个成功的步骤9个失败的尝试315个函数计算1个偏导数31个LU分解311个线性系统的解运行时间为0.081467秒。金宝搏官方网站统计ode23: 263成功步骤36失败尝试898函数评估运行时间为0.015948秒。ode113的Stats: 159成功的步骤3失败的尝试322函数评估运行时间为0.018056秒。

求解器都表现良好，但阻尼摆锤是一个非争端问题的一个很好的例子数值性能很好。在这种情况下ode15s需要做额外的工作，以获得较差的解决方案。

例2:范德堡尔振荡器

当非线性参数$\mu$较大时，范德堡尔振子方程在一定的区间内变得僵硬:

$ dot{y} - mu \left(1-y^2\right)\dot{y}+y=0$

该等式的非线性完全包含在涉及$ \ mu $的术语中：注意，如果$ \ mu = 0 $，则该等式减少了一个简单的谐波振荡器，其具有定期的周期性行为。

尝试用数值遇到了严重的阻力，需要数百万次评估和30分钟以上的执行时间(我在35分钟后停止了执行)。由于问题显然是僵硬的，这个例子比较了僵硬的求解器。

文件范德波罗德法求$\mu=1000的解ode15s，ode23s，ode23t,ode23tb.函数文件vdp1000.m随MATLAB发货，并将此方程编码为一阶ode的耦合系统:

数组$ $ \开始{}{cl} y_1 ' & = y_2 \ \ y_2 ' & = \μ\离开(1-y_1 ^ 2 \右)y_2——y_1 \{数组}$ $

提供雅可比矩阵来辅助求解，它的使用反映在偏导数计算的次数上。

函数vanderpolODE opts=odeset(“统计数据”，“上”，'雅各比亚', @J);Tspan = [0 3000];Y0 = [2 0];disp ('')，disp(“ode15s统计:) tic， [t1,y1] = ode15s(@vdp1000, tspan, y0, opts);toc disp ('')，disp(“ode23s统计:) tic， [t2,y2] = ode23s(@vdp1000, tspan, y0, opts);toc disp ('')，disp(“ode23t统计:) tic， [t3,y3] = ode23t(@vdp1000, tspan, y0, opts);toc disp ('')，disp('ODE23TB的统计数据：'）TIC，[T4，Y4] = ODE23TB（@ VDP1000，TSPAN，Y0，OPTS）;toc图形子图（2,2,1），绘图（t1，y1（：1），“o”），ylim（[ -  4 4]），标题（“ode15s”）子图（2,2,2），绘图（T2，Y2（：，1），“o”)、标题(“ode23s”)次要情节(2、2、3),情节(t3, y3 (: 1),“o”)、标题(“ode23t”)次要情节(2、2、4),情节(t4, y4 (: 1),“o”)、标题(“ode23tb”）函数dfdy=J（t，y）MU=1000；％非线性系数dfdy=[0 1-2*MU*y（1）*y（2）-1 MU*（1-y（1）^2）]；结束结束

范德波尔德

ode15s的统计:591个成功的步骤225个失败的尝试1749个函数计算45个偏导数289 LU分解1747个线性系统的解运行时间为0.192955秒。金宝搏官方网站ode23的统计:741个成功的步骤13个失败的尝试2251个函数计算741个偏导数754 LU分解2262个线性系统的解运行时间为0.092824秒。金宝搏官方网站ode23t的统计:776个成功的步骤94次失败的尝试2014函数计算36个偏导数294 LU分解2012线性系统的解运行时间为0.218996秒。金宝搏官方网站ode23tb的统计:573个成功的步骤93次失败的尝试2816函数计算44个偏导数269 LU分解3415个线性系统的解运行时间为0.202237秒。金宝搏官方网站

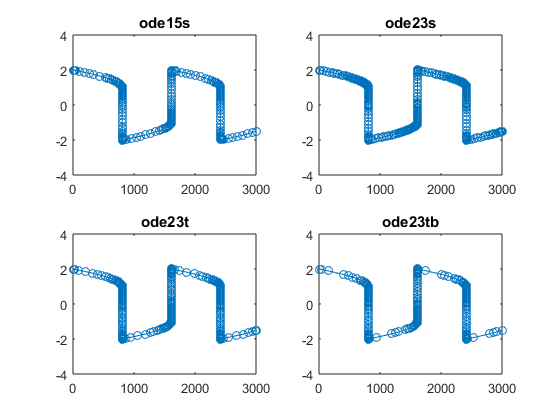
这些图是$y_1$的解。金宝搏官方网站对于这个问题,ode23s执行速度最快，失败步骤最少。提供的雅可比矩阵大大有助于ode23s在评估每个步骤中的部分衍生物。ode23tb用最少的步骤解决问题，表现出色ode15s．这个问题是一个很好的带有粗糙容忍度的刚性问题的例子ode23s和ode23tb可以表演ode15s．但实际上，所有僵硬的求解器在这个问题上都表现得很好，与之相比可以节省大量的时间数值．

总结

尽管所有的ODE求解器都能够处理相同的问题，但还是建议您从这里开始数值．然后，如果问题表现出僵硬的迹象，ode15s是一个很好的第二选择。然后，其他解算器会根据特定问题的属性以及是否可以提供额外信息（如雅可比矩阵）提供进一步的细化。

评论

你的工作是否涉及到使用MATLAB的ODE求解器?如果是，分享你的经验在这里．

进一步阅读

[1] C. moler，常微分方程用MATLAB进行数值计算电子版:MathWorks, Inc.， Natick, MA, 2004

[2]洗发腺，L. F.和M. W. Reichelt，MATLAB ODE套件暹罗科学计算杂志，第18卷，1997年。

[3] c .硅藻土常微分方程:刚度克利夫角:克利夫·莫尔数学与计算，2014

L. F.香品，常微分方程的数值解查普曼和霍尔出版社，1994年

L. F. Shampine, I. Gladwell和S. Thompson，用MATLAB求解ode，剑桥大学出版社，2003年出版社

j·d·兰伯特，常微分系统的数值方法Wiley, 1992

版权所有2015 The Mathworks，Inc。

获取MATLAB代码

发布与MATLAB®R2015a