这篇文章是我同事写的Cosmin Ionita．

的“makima”最近在R2017b发行版中引入了MATLAB®的三次插值方法，作为一种新的选项interp1，interp2，interp3，interpn,griddedInterpolant．它的实现是用户不可见的;因此，我们一直收到用户关于这种新三次方法学的详细信息的询问。

在下面，我们通过回答这些问题来解决用户的疑问:

简而言之，“makima”是修正Akima分段三次Hermite插值．它代表了对Akima导数公式的matlab特定修改，并具有以下关键属性:

内容

Akima分段三次Hermite插值

对于由节点$x$和值$v$组成的输入数据集$[x_i~x_{i+1})$，分段三次Hermite插值不仅在区间$x_i$和$x_{i+1}$上插值给定的数据值$v_i$和$v_{i+1}$，而且在$x_i$和$x_{i+1}$上有特定的导数$d_i$和$d_{i+1}$。有关更多详情，请参阅插值章在克里夫MATLAB数值计算教科书。

三次埃尔米特插值的关键是导数$d_i$的选择。

在1970年纸，秋岛浩介绍了一个导数公式避免过度的局部波动:

Akima，“一种基于局部程序的插值和平滑曲线拟合的新方法”，日本机械工程学报，v. 17-4, p.589- 602,1970。

让美元\ delta_i = \离开(v_ {i + 1} v_i \右)/ \离开(间{i + 1} -x_i \右)是间隔的斜率(美元x_i ~间{i + 1})美元。Akima在$x_i$处的导数定义为:

$ $ d_i = \压裂{| \ delta_ {i + 1} - \ delta_i | \ delta_张{}+ | \ delta_张{}- \ delta_{我2}| \ delta_i} {| \ delta_ {i + 1} - \ delta_i | + | \ delta_张{}- \ delta_{我2}|},$ $

表示区间$[x_{i-1}~x_i)$和$[x_i~x_{i+1})$的斜率$\delta_{i-1}$和$\delta_i$之间的加权平均值:

$ $ d_i = \压裂{w_1} {w_1 + w_2} \ delta_张{}+ \压裂{w_2} {w_1 + w_2} \ delta_i \,, \四\四w_1 = | \ delta_ {i + 1} - \ delta_i |, \四\四w_2 = | \ delta_张{}- \ delta_{我2}| $ $

注意，Akima在$x_i$的导数是从$x_{i-2}$， $x_{i-1}$， $x_i$， $x_{i+1}$和$x_{i+2}$这五个点局部计算出来的。对于端点$x_1$和$x_n$，它要求斜率$\delta_{-1}， \delta_0$和$\delta_n，\delta_{n+1}$。由于这些斜率在输入数据中不存在，Akima建议使用二次外推来计算它们，$\delta_0 = 2\delta_1 -\delta_2$， $\delta_{-1} = 2\delta_0 -\delta_1$和$ delta_n = 2\delta_{n-1} $， $\delta_{n -1}$， $ delta_{n+1} = 2\delta_n -\delta_{n-1}$。

但是等等!

MATLAB已经有两个立方Hermite插值方法(见Cleve的博客)样条和芯片)：

Akima的公式与之相比如何样条的而且“pchip”?

Akima的公式找到了一个很好的中间地带样条的而且“pchip”：

下面是比较这三种立方Hermite插值的典型例子:

X1 = [1 2 3 4 5 5.5 7 8 9 9.5 10];V1 = [0 0 0 0.5 0.4 1.2 1.2 0.1 0 0.3 0.6];Xq1 = 0.75:0.05:10.25;compareCubicPlots (x1, v1, xq1,假的,“不”）

改进的Akima插值——“makima”

Akima的配方当然产生了很好的效果。然而，我们还没有准备好完全采用它。

等斜率的边情况

当下斜率相等时，$\delta_{i-2} =\delta_{i-1}$，而上斜率相等时，$\delta_i =\delta_{i+1}$，分子和分母都等于0,Akima的公式返回南．Akima自己也意识到了这个问题，并建议对这种边缘情况取上下斜率的平均值:$d_i =\left(\delta_{i-1} +\delta_i \right)/2$。

让我们尝试对以下数据集进行修复，其中区间$[3~4)$和$[4~5)$具有相等的斜率$\delta_3 =\delta_4 =1$，区间$[5~6)$和$[6~7)$也具有相等的斜率$\delta_5 =\delta_6 =0$:

X2 = 1:8;V2 = [-1 -1 -1 0 1 1 1 1];Xq2 = 0.75:0.05:8.25;compareCubicPlots (x2, v2, xq2,假的,“本身”) ylim([-1.2 1.2])

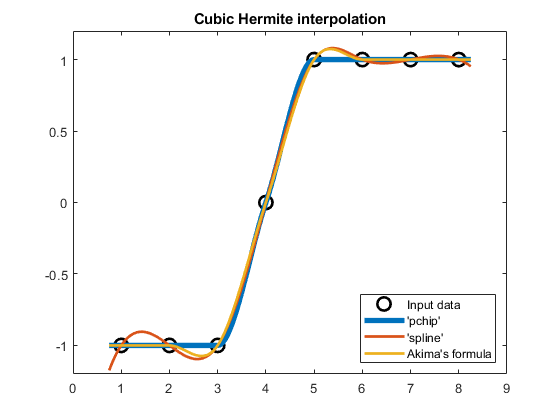
在这种情况下，阿基马南$x_5=5$处的导数替换为$d_5 =\left(\delta_4 +\delta_5 \right)/2=0.5$。

但是我们还没有准备好!

什么时候我们应该从Akima公式转换到平均公式?如果斜率是几乎等于多少?

让我们修改上面的例子，使$\delta_5 =\varepsilon$和$\delta_6 =-\varepsilon$通过设置$v_6 =1+\varepsilon$，其中$\varepsilon =2^{-52}$表示机ε．现在，我们可以将Akima的完整公式与$d_5$的平均公式进行比较，这两个数据集仅相差$\varepsilon$:

% v2eps:新数据集，仅在v2(6)中相差一个epsV2eps = v2;V2eps (6) = V2eps (6) + eps;情节(x2, v2,“柯”，“线宽”2,“MarkerSize”10“DisplayName的”，'输入数据v2')举行在情节(xq2 akima (x2, v2, xq2),“颜色”，[1 2/3 0]，“线宽”2,.．.“DisplayName的”，'v2(6) = 1使用平均公式')情节(xq2 akima (x2, v2eps, xq2),“-”。，“颜色”，[1 2/3 0]，“线宽”2,.．.“DisplayName的”，'v2(6) = 1+eps使用Akima公式')举行从传奇(“位置”，“本身”)标题(Akima插值(几乎)等边斜率) ylim([-1.2 1.2])

平均公式(实线)返回导数$d_5=0.5$，而Akima公式(虚线)返回$d_5=1$。因此，即使两个底层数据集在$v_6$处仅相差$\varepsilon$，两个Akima插值器之间在$x_5=5$附近仍存在一个不需要的、不可忽略的差异。

要求(1)

我们不希望我们的Akima插值切换到不同的公式的边缘情况。

如果超过两个连续节点的数据为常数，则超调

选择前面的例子也是为了揭示Akima插补器的另一个性质:如果连续两个以上节点的数据是常数，就像前面例子中的$v_5=v_6=v_7=1$，那么Akima插补器可能会产生一个超调，即插补器在上面$[5~6)$区间的波动。

这种特殊类型的超调量在许多工程应用中是不可取的。

对于上述$[2~3)$区间的下冲，也存在同样的担忧。

要求(2)

我们不希望Akima插值在超过两个连续节点的数据是常量时产生超调(或欠调)。

修正Akima公式

在MATLAB中,“makima”三次埃尔米特插值解决上述要求(1)和(2)。

为了消除超调并避免分子和分母都等于0的边缘情况，我们通过调整斜率$\delta_{i-1}$和$\delta_i$的权重$w_1$和$w_2$来修改Akima的导数公式:

$ $ d_i = \压裂{w_1} {w_1 + w_2} \ delta_张{}+ \压裂{w_2} {w_1 + w_2} \ delta_i \,, \四\四w_1 = | \ delta_ {i + 1} - \ delta_i | + | \ delta_ {i + 1} + \ delta_i | / 2 \四\四w_2 = | \ delta_张{}- \ delta_{我2}| + | \ delta_张{}+ \ delta_{我2}| / 2。$ $

该修正公式表示“makima”MATLAB中使用的导数公式:

让我们试试“makima”关于上述超调例子的公式:

compareCubicPlots (x2, v2, xq2,真的,“本身”) ylim([-1.2 1.2])

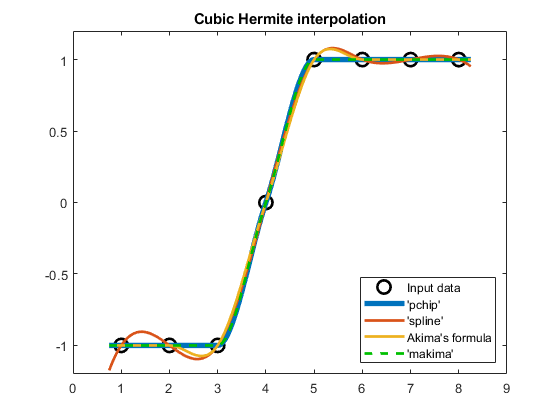
的确,“makima”如果超过两个节点的数据是常量($v_5=v_6=v_7=1$以上)，则不会产生超调。

但是这对于我们在第一个例子中看到的波动意味着什么呢?

compareCubicPlots (x1, v1, xq1,真的,“不”）

请注意,“makima”与Akima公式得到的结果非常吻合。事实上，结果如此相似，以至于很难从情节上区分它们。

因此,“makima”仍然保留了秋岛作为一个中间地带的理想属性样条的而且“pchip”就产生的波动而言。

泛化到n-D网格

但是我们还没有完成!

Akima的公式和我们的修正公式“makima”公式有另一个理想的性质:它们可以推广到高维n-D网格数据。Akima在1974年注意到这个特性纸．

H. Akima，“基于局部程序的二元插值和光滑曲面拟合方法”，ACM通讯，第17-1节，第18-20页，1974。

例如，要在二维网格$\left(x,y\right)$上进行插值，我们首先应用“makima”分别沿$x$和$y$求导公式，得到每个网格节点的两个方向导数。然后，我们还计算每个网格节点沿$xy$的交叉导数。交叉导数公式首先计算二维网格数据对应的二维除差，然后应用“makima”导数公式沿$x$对这些差值;然后，它取结果，并沿$y$应用导数公式。然后将导数和交叉导数作为表示二维插值的双变量三次埃尔米特多项式的系数代入。

同样的程序适用于$n\ ge2 $的高维n- d网格，并且需要沿所有可能的交叉方向计算交叉导数。因此,“makima”不仅在金宝appinterp1，但也在interp2，interp3，interpn,griddedInterpolant．

这是二维的“makima”插值比较2-D样条的插值生成的网格数据山峰功能:

[X1,Y1,V1] =峰值(5);[Xq1,Yq1] = meshgrid(-3:0.1:3，-3:0.1:3);Vqs1 = interp2(X1,Y1,V1,Xq1,Yq1，样条的）;冲浪(Xq1 Yq1 Vqs1)轴紧标题(”二维样条”(X1,Y1,V1,Xq1,Yq1，“makima”）;冲浪(Xq1 Yq1 Vqm1)轴紧标题(“二维“makima””）

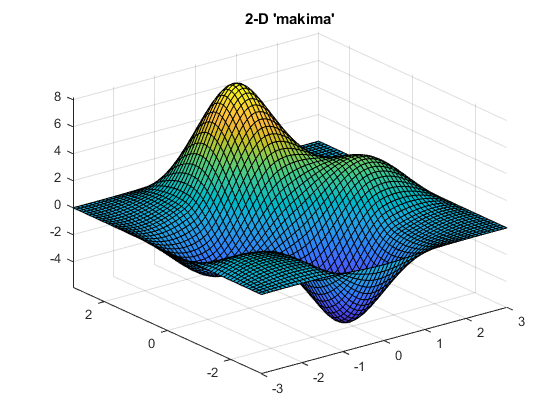
注意产生的较小的波动(或摆动)“makima”．

最后，让我们试试“makima”在一个有一些2-D峰值的例子中，数据有锐利的边缘和台阶:

V2 = 0 (10);V2(2:5,2:5) = 3/7;%第一步V2(6:7,6:7) = [1/4 1/5;1/5 1/4);%中间步骤V2(8:9,8:9) = 1/2;%最后一步V2 = flip(V2,2);[Xq2,Yq2] =网格(1:0.2:10,1:0.2:10);Vqs2 = interp2(V2,Xq2,Yq2，样条的）;冲浪(Xq2 Yq2 Vqs2)轴紧标题(”二维样条”) Vqm2 = interp2(V2,Xq2,Yq2“makima”）;冲浪(Xq2 Yq2 Vqm2)轴紧标题(“二维“makima””）

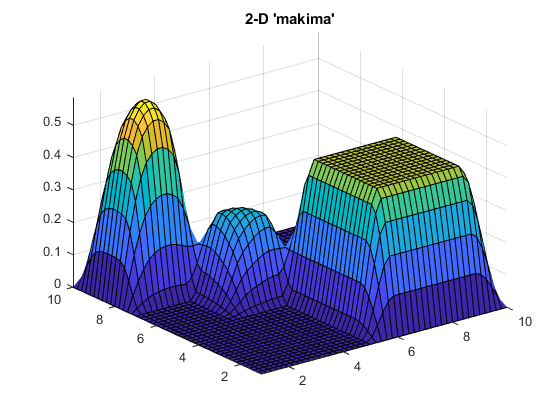
的“makima”结果具有较小的波动(或摆动)样条。

总结

最后，我们总结了MATLAB支持的三种立方Hermite插值方法的相关性质:金宝app

摘要=表(.．.［“C2”；“使用所有点”；“Not-a-knot条件”；“是的”),.．.［“C1”；“用4分”；“单边坡”；“不”),.．.［“C1”；“用5分”；“二次推断”；“是的”),.．.“VariableNames”，.．.［“样条”“pchip”“makima”),.．.“RowNames”，.．.［“连续性”；“位置”；“终点”；“金宝app支持一天”]);disp(总结)

花键pchip makima  ______________________ _________________ _________________________ 连续性”C2”“C1”“C1”地区“使用所有点”“使用4点”“使用5点“端点”Not-a-knot条件”“单边坡”“二次推断”支持一天“是”“否”“是”金宝app

代码

compareCubicPlots

函数compareCubicPlots (x, v, xq, showMakima legendLocation)绘制“pchip”、“样条”、Akima和“makima”插值结果VQP = pchip(x,v,xq);%等同于vq = interp1(x,v,xq，'pchip')VQS =样条(x,v,xq);%等同于vq = interp1(x,v,xq，'样条')Vqa = akima(x,v,xq);如果showMakima vqm = makima(x,v,xq);%等同于vq = interp1(x,v,xq，'makima')结束情节(x, v,“柯”，“线宽”2,“MarkerSize”10“DisplayName的”，输入数据的)举行在情节(vqp xq,“线宽”4“DisplayName的”，“pchip”)情节(xq,矢量量化,“线宽”2,“DisplayName的”，“样条”)情节(xq,酒瓶,“线宽”2,“DisplayName的”，Akima”年代公式）如果vqm showMakima情节(xq,“——”，“颜色”，[0 3/4 0]，“线宽”2,.．.“DisplayName的”，“makima”）结束持有从xticks (x (1) 1: x(结束)+ 1)传说(“位置”legendLocation)标题(“三次赫米特插值”）结束

akima

函数Vq = akima(x,v,xq)AKIMA AKIMA分段立方Hermite插值。％% vq = AKIMA(x,v,xq)在查询点xq处插入数据(x,v)%使用Akima的立方埃尔米特插值公式。％%的引用:％% H. Akima，“一种插值和平滑曲线拟合的新方法。《基于本地程序的方法》，《中华医学会杂志》，1970年第17-4期，第589-602页。％AKIMA vs. PCHIP vs. SPLINE:％% - Akima的立方公式是样条和PCHIP之间的中间地带:它具有比样条更低的振幅摆动，但不像样条那样激进%在减少摆动的PCHIP。% - Akima的三次公式和样条推广到n-D网格。％例如:比较AKIMA和MAKIMA、SPLINE和PCHIP％% x = [1 2 3 4 5 5.5 7 8 9 9.5 10];% v = [0 0 0 0.5 0.4 1.2 1.2 0.1 0 0.3 0.6];% xq = 0.75:0.05:10.25;% VQS =样条(x,v,xq);% VQP = pchip(x,v,xq);% vqa = akima(x,v,xq);% VQM = makima(x,v,xq);％%图% plot(x,v，'ko'，'LineWidth'，2，'MarkerSize'，10)，稍候%的阴谋(vqp xq,“线宽”,4)%的阴谋(vq xq, xq,酒瓶,xq, vqm,“——”,“线宽”,2)%传奇(“数据”,“pchip””,“样条“”、“Akima”年代公式”,“‘makima“”)% title(' MATLAB中的立方厄米特插值')％参见MAKIMA, SPLINE, PCHIP。% mailto: cosmin.ionita@mathworks.com断言(isvector (x) & & isvector (v) & &(元素个数(x) = =元素个数(v)))断言(元素个数(x) > 2) x = x(:)。';V = V (:).';%与pchip中的形状相同。M和样条。M计算Akima斜率H = diff(x);Delta = diff(v)./h;斜坡= akimaSlopes(delta);求分段三次Hermite插值Vq = ppval(pwch(x,v,slope,h,delta)，xq);结束

akimaSlopes

函数s = akimaSlopes(delta)% Akima立方Hermite插值的导数值Akima在网格节点x(i)上的导数估计需要四个有限5个网格节点x(i-2:i+2)对应的差异百分比。％对于边界网格节点x(1:2)和x(n-1:n)，附加有限差分%，对应于x(-1:0)和x(n+1:n+2)%非中心差分公式对应二次外推%使用由x(1:3)处的数据定义的二次多项式% (Akima论文第2.3节):N =数字(delta) + 1;%网格节点数xDelta_0 = 2*delta(1) - delta(2);Delta_m1 = 2*delta_0 - delta(1);Delta_n = 2* (n-1) - (n-2);Delta_n1 = 2*delta_n - delta(n-1);Delta = [delta_m1 delta_0 Delta delta_n delta_n1];% Akima导数估计公式(文中式(1)):％% H. Akima，“一种插值和平滑曲线拟合的新方法。《基于本地程序的方法》，《中华医学会杂志》，1970年第17-4期，第589-602页。％% s (i) = (| d - d (i + 1)(我)| * d(张)+ | d(张)- d(我2)| * d(我))(|d(i+1)-d(i)| + |d(i-1)-d(i-2)|)权重= abs(diff(delta));Weights1 = weights(1:n);% | d - d(我2)|(张)Weights2 = weights(3:end);% | d (i + 1) - d(我)|Delta1 = (2:n+1);% d(张)Delta2 = delta(3:n+2);% d(我)Weights12 = weights1 + weights2;S = (weights2./weights12) .* delta1 + (weights1./weights12) .* delta2;为了避免0/0,Akima建议对分割后的差异d(i-1)进行平均对于d(i-2) = d(i-1)和d(i) = d(i+1)的边情况，%和d(i):Ind = weights1 == 0 & weights2 == 0;S (ind) = (delta1(ind) + delta2(ind)) / 2;结束

makima

函数Vq = makima(x,v,xq)修正Akima分段三次Hermite插值。％我们修改了Akima的公式以消除超调和欠调。%，当连续两个以上节点的数据不变时。％% vq = MAKIMA(x,v,xq)在查询点xq处插入数据(x,v)%使用改进的Akima立方Hermite插值公式。％%的引用:％% H. Akima，“一种插值和平滑曲线拟合的新方法。《基于本地程序的方法》，《中华医学会杂志》，1970年第17-4期，第589-602页。％% MAKIMA vs. PCHIP vs. SPLINE:％% - MAKIMA是SPLINE和PCHIP之间的中间地带:它具有比样条更低的振幅摆动，但不像样条那样激进%在减少摆动的PCHIP。% - MAKIMA和样条推广到n-D网格。％示例:当数据为时，使用MAKIMA没有超调和欠调%常数，用于连续两个以上节点％% x = 1:7;% v = [-1 -1 -1 0 1 1 1];% xq = 0.75:0.05:7.25;% VQS =样条(x,v,xq);% VQP = pchip(x,v,xq);% vqa = akima(x,v,xq);% VQM = makima(x,v,xq);％%图% plot(x,v，'ko'，'LineWidth'，2，'MarkerSize'，10)，稍候%的阴谋(vqp xq,“线宽”,4)%的阴谋(vq xq, xq,酒瓶,xq, vqm,“线宽”,2)%的传说(“数据”,“pchip”’,”样条“”、“Akima”年代公式”,…%”makima””、“位置”、“SE”)% title(" 'makima "在x(1:3)和x(5:7)中没有超调')％例如:比较MAKIMA和AKIMA、SPLINE、PCHIP％% x = [1 2 3 4 5 5.5 7 8 9 9.5 10];% v = [0 0 0 0.5 0.4 1.2 1.2 0.1 0 0.3 0.6];% xq = 0.75:0.05:10.25;% VQS =样条(x,v,xq);% VQP = pchip(x,v,xq);% vqa = akima(x,v,xq);% VQM = makima(x,v,xq);％%图% plot(x,v，'ko'，'LineWidth'，2，'MarkerSize'，10)，稍候%的阴谋(vqp xq,“线宽”,4)%的阴谋(vq xq, xq,酒瓶,xq, vqm,“——”,“线宽”,2)%传奇(“数据”,“pchip””,“样条“”、“Akima”年代公式”,“‘makima“”)% title(' MATLAB中的立方厄米特插值')％参见AKIMA，样条，PCHIP。% mailto: cosmin.ionita@mathworks.com断言(isvector (x) & & isvector (v) & &(元素个数(x) = =元素个数(v)))断言(元素个数(x) > 2) x = x(:)。';V = V (:).';%与pchip中的形状相同。M和样条。M计算修改的Akima斜率H = diff(x);Delta = diff(v)./h;斜坡= makimaSlopes(delta);求分段三次Hermite插值Vq = ppval(pwch(x,v,slope,h,delta)，xq);结束

makimaSlopes

函数s = makimaSlopes(delta)%修正Akima立方Hermite插值的导数值Akima在网格节点x(i)上的导数估计需要四个有限5个网格节点x(i-2:i+2)对应的差异百分比。％对于边界网格节点x(1:2)和x(n-1:n)，附加有限差分%，对应于x(-1:0)和x(n+1:n+2)%非中心差分公式对应二次外推%使用由x(1:3)处的数据定义的二次多项式% (Akima论文第2.3节):N =数字(delta) + 1;%网格节点数xDelta_0 = 2*delta(1) - delta(2);Delta_m1 = 2*delta_0 - delta(1);Delta_n = 2* (n-1) - (n-2);Delta_n1 = 2*delta_n - delta(n-1);Delta = [delta_m1 delta_0 Delta delta_n delta_n1];% Akima导数估计公式(文中式(1)):％% H. Akima，“一种插值和平滑曲线拟合的新方法。《基于本地程序的方法》，《中华医学会杂志》，1970年第17-4期，第589-602页。％% s (i) = (| d - d (i + 1)(我)| * d(张)+ | d(张)- d(我2)| * d(我))(|d(i+1)-d(i)| + |d(i-1)-d(i-2)|)％%以消除超调和欠调时，数据是常数为更多%比两个连续的节点，在MATLAB的'makima'中我们修改Akima的通过在权重中添加额外的平均项来计算%公式。% s (i) = ((| d - d (i + 1)(我)| + | d (i + 1) + d (i) | / 2) * d(张)+% (|d(i-1)-d(i-2)| + |d(i-1)+d(i-2)|/2) * d(i))% / (|d(i+1)-d(i)| + |d(i+1)+d(i)|/2)+% (|d(i-1)-d(i-2)| + |d(i-1)+d(i-2)|/2)权重= abs(diff(delta)) + abs((delta(1:end-1)+delta(2:end))/2);Weights1 = weights(1:n);% | d - d(我2)|(张)Weights2 = weights(3:end);% | d (i + 1) - d(我)|Delta1 = (2:n+1);% d(张)Delta2 = delta(3:n+2);% d(我)Weights12 = weights1 + weights2;S = (weights2./weights12) .* delta1 + (weights1./weights12) .* delta2;%如果连续4个以上节点的数据不变，则%分母为零，公式产生一个不需要的NaN结果。将此NaN替换为0。S (weights12 == 0) = 0;结束

版权所有2019 The MathWorks, Inc.
获取MATLAB代码

发布与MATLAB®R2018b