我首先调查了力量之塔

$ $ z ^ {z ^ {z ^ z}} $ $

那时我还在上初中，大概十四五岁。我每隔几十年就会回去看看。这是另一集。

内容

结合性

做

$ $ 2 ^ 3 ^ {4} $ $

的意思是

$ $ {(2 ^ 3)} ^ 4 = 8 ^ 4 = 2 ^ {12}, \ \ mbox{或}\ 2 ^ {(3 ^ 4)}= 2 ^ {81}$ $

这有很大的不同。

加法和乘法是结合的。我们的意思是

2 * 3 * 4

ans = 24

都可以计算出来吗

(2 * 3) * 4

ans = 24

或

2 * (3 * 4)

ans = 24

它们是一样的。

但是减法、除法和取幂是不能结合的。MATLAB从左到右关联。所以

格式老鼠2/3/4

ans = 1/6

计算了

(2/3) / 4

ans = 1/6

而不是

2 / (3/4)

ans = 8/3

数学大会

取幂法通常的数学惯例是正确的结合性。

$ a^{b^c} = a^{(b^c)} $

这是因为左结合律可以用乘法代替。

$ (a^ {b)}^c = a^{bc} $

所以，我的力量之塔是

$ z^{z^{z^z}} = z^{(z^{(z^z)})} $

我想让这个塔无限高。

WS算法

我一直在用上标和括号来扩大我的印刷运气。让我们安定下来。

对于给定的$z$，设$y$在最后一段末尾表示塔的无限延伸。然后，因为它是无限的，并且与右边相关联，我们有

$ y = z^y $

这样至少更容易排版了。

有一个很明显的方法来计算它。我称之为WS或世界上最简单的算法。

$ y_1 = 1 $$

$$ mbox{for} \ n = 1，…， \ \ y_{n+1} = z^{y_n} $

当然，这个更广为人知的名字是不动点算法

$ y_{n+1} = f(y_n) $

函数的

$ f(z) = z^y $。

两个实验

让我们试一下$z$的两个不同值，$1.25$和$1.5 $。

格式长y = 1为N = 1:30 y = z^y;disp (y)结束snapnow

z = y = 1 1.250000000000000 1.250000000000000 1.321714079300705 1.343034993578008 1.349439873733169 1.351369882459350 1.351952000918108 1.352127625454628 1.352180615675240 1.352196604529415 1.352201428918186 1.352202884606055 1.352203323838621 1.352203456370664 1.352203496360284 1.352203508426572 1.352203512067399 1.3522035131659661.352203513640443 1.352203513640661 1.3522035136406640 1.352203513636746 1.352203513639493 1.352203513640323 1.352203513640573 1.352203513640648 1.352203513640671 1.352203513640678 1.352203513640681

格式长Z = 1.5 y = 1为N = 1:15 y = z^y;disp (y)结束snapnow

z = 1.500000000000000 y = 1 1.500000000000000 1.837117307087384 2.106203352148880 2.349005318611934 2.592025704907509 2.860441497460648 3.189324761899238 3.644283987904574 4.382546732246116 5.911914873330858 10.990982932689437 86.181891743310985 1.499263005586202e+15 Inf Inf

它收敛于$z = 1.25$，但不收敛于$z = 1.5$。在1.25美元到1.5美元之间发生了一些重要的事情。

√6 (2)

我们试试$z =根号{2}$

格式长Z =根号2 y = 1为N = 1:30 y = z^y;disp (y)结束

z = y = 1 1.414213562373095 1.414213562373095 1.632526919438153 1.760839555880029 1.840910869291011 1.892712696828511 1.926999701847101 1.950034773805818 1.965664886517319 1.976341754409703 1.983668399303822 1.988711773413954 1.992190882947058 1.994594450712102 1.996256666265859 1.997407001141337 1.998203477508703 1.9987551330845931.999137310119392 1.999402118324998 1.999585622935682 1.9999712796329641 1.999800935492971 1.999862023757784 1.999904364443337 1.999933711582101 1.999954052897822 1.999968152149245 1.999977924873871 1.999984698747096 1.999989394007813

它收敛于$y = 2$，因为这是一个不动点。

$$(√{2})^2 = 2 $$

所以关键是在1.4美元和1.5美元之间。

最高的塔

我记得当我第一次知道$z$的最大可能值只比$\根号{2}$大一点时，我非常着迷。这是一个惊人的数量

$ mbox{e}} = $ mbox{e}^{1/ mbox{e}} $

ebar = exp (1) ^ exp (1)

ebar = 1.444667861009766

这是因为$\bar{\mbox{e}}$是另一个不动点。

$ $ \酒吧{\ mbox {e}} ^ {\ mbox {e}} = (\ mbox {e} ^ {1 / {\ mbox {e}}}) ^ {\ mbox {e}} = \ mbox {e} $ $

让我们看看为什么$ bar{\mbox{e}}$是$z$的最大可能值。

分析

利用均值定理对WS算法进行了分析。

$ $ f(最大)= f (y_ {n}) + f (\ xi_n) (y_n-y_ {n}) $ $

对于$y_n$和$y_{n-1}$之间的$\xi_n$。

在我们的例子中，$f'(z) = ln{z}\ z^y$，所以

$ $ y_ {n + 1} =最大+ (\ ln {z}) (z ^ {\ xi_n}) (y_n-y_ {n}) $ $

这告诉我们

$ |y_{n+1}-y_n| \le C |y_n-y_{n-1}|$$

的数量

$ mbox{max} |\ln{z}||z^y|$$

在包括迭代的区域中，最大值是在$y$ s和$z$ s之上。如果$C$小于1，迭代会更接近，所以迭代是a收缩这是收敛的。

让我们做一个数值搜索，绘制$(ln{z})(z^y)$的等高线图。在$C$小于$1$的区域使用绿色，在$C$大于1的区域使用红色和蓝色。

[Z, Y] = ndgrid (. 01: .01:2.0 . 01: .01:4.0);R =日志(Z)。* Z ^ Y;contourf (Z, Y, R, [25:4: 1 1:20:21]);Colormap ([0 0 .75;0 .75 .25; 10 0 0]);e = exp (1);线([ebar ebar], [e],“标记”，“。”，“markersize”, 24岁,“颜色”，“黄色”甘氨胆酸)组(,“xtick”,(。011/e 1 e^(1/e) 2]) set(gca,“xticklabel”，{' 0 '，“1 / e”，' 1 '，“e ^ (1 / e)”，' 2 '})集(gca,“ytick”,(。0112e 4]) set(gca,“yticklabel”，{' 0 '，' 1 '，' 2 '，“e”，“4”})包含(“z”), ylabel (“y”)轴广场

稳定塔

如果我们停留在绿色区域，其中$C$小于1,WS迭代收敛，塔是稳定的。这包括区间内$z$的所有值

$ {1/\mbox{e} \le z \le mbox{e}^{1/\mbox{e}} $

塔倒塌

我在初中遇到的关键值是黄色圆点$z=\bar{\mbox{e}}=\mbox{e}^{1/ mbox{e}}$和$y=\mbox{e}$。当我们从稳定区域接近点时，$f'(z)$接近$f'(\bar{\mbox{e}})=1$， WS算法的收敛速度非常慢。

在$z=\bar{\mbox{e}}$的右边，迭代会在C大于1的红色危险区域遇到$y$的值，所以它会迅速发散，塔很快就会倒塌，就像我们在$z=1.5$看到的那样。

小z

$z$小于$1/\mbox{e}$的值，大约是$0.37$，稍微微妙一些。我们可能在蓝色区域，也可能不在。结果表明，$z$大于$ mbox{e}^{\mbox{-e}}$(约为$0.066$)的值，仍然会遇到足够大的$y$，使迭代保持在安全的绿色区域，因此它收敛。

但是现在尝试$z = 0.05$进行一些迭代。

Z = 0 y = 1为K = 1:20, y = z^y;disp (y),结束

z = y = 1 0.050000000000000 0.050000000000000 0.860891659331735 0.075849745545982 0.796741072475616 0.091921259400909 0.759290007184149 0.102834993569945 0.734866735033395 0.110641061786732 0.717881331845427 0.116416584607138 0.705567440560545 0.120791283462031 0.696381005849372 0.124161635028397 0.689385252311344 0.1267911988280700.683975974940914 0.128862555680671 0.679744887323325

它看起来并不想收敛。在没有任何输出的情况下运行300多个迭代。

为K = 1:300, y = z^y;结束

现在检查一下在总共320次迭代之后我们做得如何。

为K = 1:10, y = z^y;disp (y),结束

0.137359395737956 0.662660838900549 0.137359395737956 0.662660838900549 0.137359395737956 0.662660838900549 0.662660838900549 0.662660838900549

它已经形成了一种模式，在两个值之间来回振荡。这是一个简单的例子期翻倍分岔．

这是所有$z$小于$ mbox{e}^{mbox{-e}}$的行为。遇到的$y$的值将我们放在蓝色区域。不动点迭代不是收缩。它稳定地进入两个循环。两个极限点之间的距离随着$z$变小而增加。

基于$z$小于$\mbox{e}^{\mbox{-e}}$的塔的奇数层是一个高度，偶数层是另一个高度。

进入兰伯特W

这是另一种看待权力之塔的方式。它涉及到朗伯W函数我以前的博客．

$ y = z^y = mbox{e}^{y\ln{z}} $

$ mbox{e}^{-y\ln{z}} = 1

$ -y\ln{z} {-y\ln{z}} = - ln{z} $

$ W(- ln{z}) = W(- ln{z}) $

$ W(- ln{z})}{- ln{z}} $

因此，朗伯W函数为任意$z$提供了无限塔的值。我上初中的时候不知道这些。

塔的功能

让我们用这个公式来计算$z$的一些值，包括一些小于$\mbox{e}^{\mbox{-e}}$的值。

T = @ (z) Lambert_W(日志(z))。/(日志(z)) z =[1.25倍根号(2)ebar 1.5 e ^ (- e) 0.05 10 ^ (- (3:3:15))) ';disp (“z T (z)”) disp (T (z) [z])

T = @ (z) Lambert_W(日志(z))。/(日志(z)) z T (z) 1.250000000000000 1.352203513640681 1.414213562373095 2.000000000000000 1.444667861009766 2.718281787975775 1.500000000000000南0.065988035845313 0.367879441171442 0.050000000000000 0.350224852743194 0.001000000000000 0.219513151627722 0.000001000000000 0.141526856553182 0.0000000010000000.107583717152717 0.000000000001000 0.087971500166559 0.000000000000001 0.074997053328098

情节

现在是一个情节。

ezplot(T，[0 ebar])轴([0 ebar 0 e])标题(“权力的塔”）

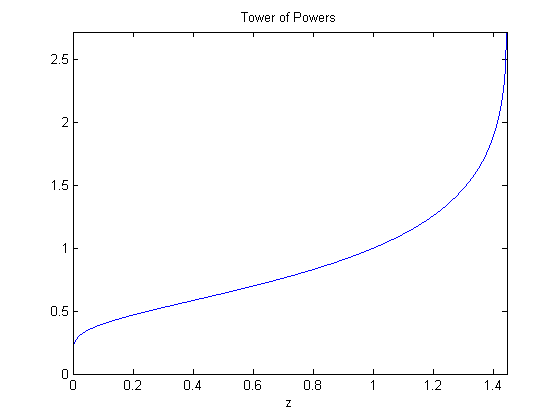
不稳定

由Lambert W公式得到的$y$的值是$f(z)$的不动点，但可能是不稳定点。如果我们的值$z$小于$ mbox{e}^{\mbox{-e}}$并且我们从Lambert W公式给出的$y$的值开始不动点算法，它将保持在那里。但是如果我们从任何其他值$y$开始，迭代器最终会找到分支吸引子对。

获取MATLAB代码

发布与MATLAB®R2013b

发布与MATLAB®R2013b