当我在写关于贬义的集合管，我很高兴地发现，在计算三次Kronecker乘积的特征值时，舍入误差产生了有趣的模式。下载188bet金宝搏

内容

克罗内克积

两个矩阵$A$和$B$的克罗内克乘积，表示为$A \otimes B$，计算为克隆亚麻(A, B)，是包含$B$元素与$A$元素的所有可能乘积的大矩阵。下载188bet金宝搏

$ $ \ otimes B = \离开(\{数组}{rrrr}开始现代{1 1}B &现代{1,2}B &……& a_{1,n}B \\ a_{2,1}B & a_{2,2}B &…& a_{2,n}B \\…\\ a_{m,1}B & a_{m,2}B &…$$ . $ (a, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B, B

两个矩阵$A \otimes B$和$B \otimes A$是不相等的，尽管它们在不同的顺序中有相同的元素。

这两个矩阵$A \otimes (B \otimes C)$和$(A \otimes B) \otimes C$相等。这是三克罗内克积$A \otimes B \otimes C$。

$A × B$的特征值是$A$和$B$的特征值的所有可能的乘积。下载188bet金宝搏

例子

例如，假设$A$是幻方。

$$ A = left(\begin{array}{rrr} 8 & 1 & 6 \\ 3 & 5 & 7 \\ 4 & 9 & 2 \end{array} \right)

$I$是单位矩阵。

左($ $ I = \ \{数组}{rr}开始结束1 & 0 0 & 1 \ \ \{数组}\右)$ $

那么$I \otimes A$是块对角线，在对角线上有$A$的副本。

$ $我左\ otimes A = \ \{数组}{rrrrrr}开始8 & 1 & 6 & 0 & 0 & 0 \ \ 3 & 5 & 7 & 0 & 0 & 0 \ \ 4 & 9 & 2 & 0 & 0 & 0 \ \ 0 8 & 0 & 0 & & 1 & 6 \ \ 0 & 0 & 0 & 3 & 5 & 7 \ \ 0 & 0 & 0 & 4 & 9 & 2 \结束数组{}\右)$ $

$A \otimes I$有$A$的元素沿多个对角线分布。

$ $我= \ \ otimes左(\{数组}{rrrrrr}开始8 & 0 & 1 & 0 & 6 & 0 \ \ 0 8 & 0 & & 1 & 0 & 6 \ \ 3 & 0 & 5 & 0 & 7 & 0 \ \ 0 & 3 & 0 & 5 & 0 & 7 \ \ 4 & 0 & 9 & 0 & 2 & 0 \ \ 0 & 4 & 0 & 9 & 0 & 2 \结束数组{}\右)$ $

$A\otimes I$和$I \otimes A$的特征值都是$A$的特征值的多个副本。

一个=魔法(3);我眼睛= (2);eig_A = eig(kron(I,A)) eig_IxA = eig(kron(A,I))

eig_A = 15.000000000000004 4.898979485566361 -4.898979485566358 eig_IxA = 15.000000000000004 4.898979485566361 -4.898979485566358 15.000000000000004 4.898979485566361 -4.898979485566358 eig_AxI = 4.898979485566356 -4.898979485566355 15.000000000000002 - 14.999999999999998 4.898979485566359 - -4.898979485566356

具有高多重性的特征值

我们的积木是多项式的同伴矩阵

$ $ $ $ ^ p (s ^ 2 - 1)

展开涉及二项式系数。例如,p= 4,

$ (s^2-1)^4 = s^8 - 4 (s^ 6) + 6 (s^ 4) - 4 (s^2 + 1) $

这是矩阵的特征多项式

(4) =伙伴

= 0 4 0 6 0 4 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0

的特征值一个+1和-1是重复的吗p次;这是他们的代数多重性．他们的几何重数只有一个;它们各自只有一个特征向量。

特征值对任何类型的误差都非常敏感，包括舍入误差。

格式长e = eig (A)

e = -1.000063312800363 + 0.000063312361825我-1.000063312800363 - 0.000063312361825我-0.999936687199636 + 0.000063313248591 -0.999936687199636 - 0.000063313248591 1.000078270656946 0.999999997960933 + 0.000078268622898 + 0.000000000000000我0.999999997960933 - 0.000078268622898我0.999921733421185 + 0.000000000000000

精确的特征值可以用

确切=圆(e)

Exact = -1 -1 -1 -1 1 1 1 1 1 1 1 1 1

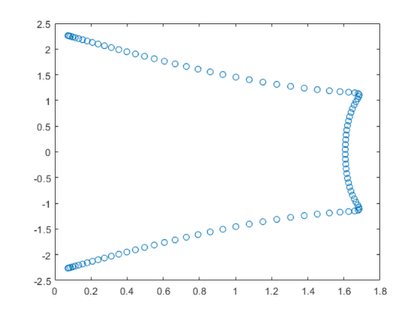
计算的特征值位于复平面的圆上，以精确的值为中心，半径大致为p-舍入误差的第一个根。在这个例子中，以+1为中心的值恰好比以-1为中心的值更精确。

half_fig eigplot (e) eigplot (+ 1, e)

菲德勒同伴矩阵

传统的伴侣矩阵的另一种选择是菲德勒同伴矩阵。

=同伴(4菲德勒的）

= 0 4 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 4 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0

这次特征值的计算顺序是相反的，在-1是更准确的。

e = eig (A)

e = 1.000107000301506 + 0.000000000000000我1.000000000805051 + 0.000107001107366 1.000000000805051 - 0.000107001107366 0.999892998088390 0.000000000000000 -1.000062156379228 + 0.000000000000000 + -0.999999990704846 + 0.000062147083463我-0.999999990704846 - 0.000062147083463我-0.999937862211083 + 0.000000000000000

e = flipud (e);half_fig eigplot (e) eigplot (+ 1, e)

三克罗内克积

我们的图形TKP包括$K$，三重克罗内克矩阵乘积

$ K = A × I × B $$

其中$A$和$B$是多项式$(s^2-1)^p$和$(s^2-1)^r$的同伴矩阵，$I$是$q$ -by- $q$的单位矩阵。

p, q和r的值是由控件设置的。一开始是4 3 2。$K$的大小是这三种尺寸的乘积的4倍，n = 4pqr。计算时间为$O(n^3)$。n的值可能大于4000，但速度很慢。

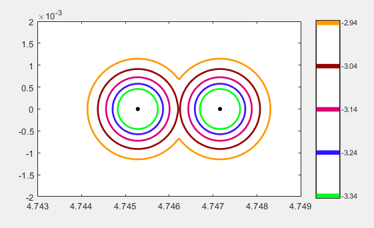
$K$的特征值有一半等于+1，另一半等于-1，所以这些特征值有很高的多重性，并且对舍入误差非常敏感。显示器显示计算值和准确的特征值之间的差异。$K$的结构使得这些错误在复杂平面的许多不同的圆上产生挑衅性的图案。

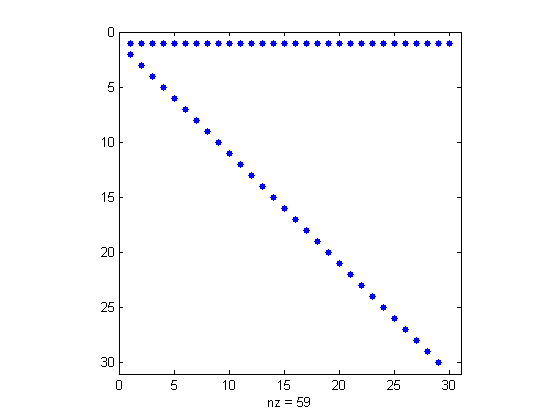
有两种不同舍入行为的配对矩阵。传统的伴矩阵的所有多项式系数都在上海森贝格矩阵的第一行。费德勒伴矩阵的系数排列在五对角矩阵的上对角线和次对角线上。

TKP

这是计算的核心。完整的程序与控制可在这里:tkp.m．

函数tkp(p,q,r) A = companion(p);我眼睛= (q);B =同伴(r);K = kron (A,克隆亚麻(我,B));e = eig (K);确切=圆(e);Err = e - exact;情节(呃,“。”）结束

函数c = 1;为J = 1: c = conv(c，[1 0 -1]);结束m = 2 * p;X = (- c (2: m + 1);眼睛(m - 1 m));结束

获取MATLAB代码

发布与MATLAB®R2019b