このページの翻訳は最新ではありません。ここをクリックして,英語の最新版を参照してください。
线形代数
MATLAB环境の行列
このトピックでは,MATLAB®で行列を作成し,基本的な行列演算を行う方法を紹介します。
MATLAB環境では,“行”列という用語を使って,2次元グリッドに配置された実数または複素数を含む変数を示します。“配列” とは一般的に数値のベクトル,行列または高次元グリッドです.MATLABのすべての配列は四角形になり,すべての次元の成分は同じ长さになります。行列で定义される数学演算は,线形代数で取り扱う内容です。
行列の作成
MATLABには、さまざまな行列を作成する関数が多数用意されています。たとえば、パスカルの三角形に基づくエントリを含んだ対称行列を作成することができます。
一个=帕斯卡(3)
A = 1 1 1 1 2 3 1 3 6
または,行方向と列方向の和が等しい非対称の“魔方阵行列” を作成することもできます。
B =魔法(3)
B = 8 1 6 3 5 7 4 9
もう1つの例は,ランダムな整数からなる3行2列の方形行列です。ここでは,兰迪への最初の入力が整数値の取り得る範囲を示し、次の 2.つの入力が行と列の数を示します。
C =兰迪(10、3、2)
C = 9 10 10 7 2
列ベクトルはm行1列の行列,行ベクトルは1行n列の行列,スカラーは1行1列の行列です。行列を手動で定義するには,大かっこ[]を使用して配列の先头と末尾を示します。大かっこ内で行末を示すには,セミコロン;を使用します。スカラー(1行1列の行列)の場合,大かっこは不要です。たとえば,以下のステートメントは列ベクトル、行ベクトル、およびスカラーを生成します。
u = [3;1;4] V = [2 0 -1] S = 7
U = 3 1 4 v = 2 0 -1 s = 7
行列の作成と取り扱い方法の详细は,行列の作成、連結、および拡張を参照してください。
行列の加算と減算
行列と配列の加算および减算は要素ごとに,すなわち“要素単位“で実行されます。たとえば,A.をBに加算し,その结果からA.を減算するとBに戻ります。
X = A + B
X = 9 2 7 4 7 10 5 12 8
Y = X - 甲
Y = 8 1 6 3 5 7 4 9 2
加算と減算では,両方の行列の次元に互換性がなければなりません。次元に互換性がない場合はエラーになります。
X = A + C
错误使用+矩阵尺寸必须一致。
詳細については,配列と行列の演算を参照してください。
ベクトル積と転置
同じ長さの行ベクトルと列ベクトルの乗算は、順番を変えても計算結果は同じになります。結果は、“内积” と呼ばれるスカラーか,“外积” と呼ばれる行列のいずれかになります。
u = [3;1;4);V = [2 0 -1];X = V * U
x = 2
X = U * V
X = 6 0 -3 2 0 -1 8 0 -4
実数行列の"転置" 演算では、A.IJ.と一吉を交換します。複素数行列の場合,もう1つの考慮事項は,配列内の複素数エントリの複素共役から”複素共役転置”を形成するかどうかです。MATLABはアポストロフィ演算子 (')を使用して复素共役転置を行い,ドットアポストロフィ演算子(。) を使用して共役なしの転置を行います。すべての要素が実数の行列では、これら 2.つの演算子の処理は同じになります。
例の行列一个=帕斯卡(3)は"対称" であるため、A'はA.と等しくなります。しかし,B =魔法(3)は対称でないため,B'の各要素は主対角に対し鏡像の位置になります。
B =魔法(3)
B = 8 1 6 3 5 7 4 9
X = B”
X = 8 3 4 1 5 9 6 7 2
ベクトルの场合,転置によって行ベクトルは列ベクトル(またはその逆)になります。
X = V” X = 2 0 -1
xとYが共に実数の列ベクトルの場合,積x*yは定义されません。ただし,次の2つの积,
x ' * y
と
y'*x
は同じスカラーの結果を生成します。これらは使用頻度が高く,“内” 积,”“スカラー積,“ドット” 积と呼ばれています。点という名前の,ドット积専用の关数も用意されています。
複素数ベクトルや行列Zに対して,Z”は複素共役転置を表します。すなわち,各要素の虚数部の符号が逆になります。たとえば,次の複素行列を考えます。
Z = [1 + 2I 7-3i 3 + 4I;6-2i 9I 4 + 7I]
Z = 1.0000 + 2.0000i 7.0000 - 3.0000i 3.0000 + 4.0000i 6.0000 - 2.0000i 0.0000 + 9.0000i 4.0000 + 7.0000i
Zの複素共役転置は次のようになります。
Z”
ANS = 1.0000 - 2.0000i 6.0000 + 2.0000i 7.0000 + 3.0000i 0.0000 - 9.0000i 3.0000 - 4.0000 4.0000i - 7.0000i
各要素の虚数部がその符号を保持し,共役を取らない複素転置はZ“。で定义します。
Z“。
ANS = 1.0000 + 2.0000i 6.0000 - 2.0000i 7.0000 - 0.0000 3.0000i + 9.0000i 3.0000 + 4.0000i 4.0000 + 7.0000i
复素ベクトルに対して2つのスカラー积x ' * yとy'*xは互いに复素共役で,スカラー积x ' * xは実数です。
行列の乘算
行列の乗算は,線形変換の構成を反映するように定義されており,線形方程式を簡潔に表現できます。行列積 C = AB は、A の列の次元が B の行の次元と等しいとき、またはどちらかがスカラーの場合に定義されます。A が m 行 p 列で、B が p 行n 列の行列の場合、積 C は m 行 n 列の行列になります。積は、実際には MATLAB の为了ループ,结肠表記,ベクトルのドット積を使って定義できます。
A =帕斯卡(3);B =魔法(3);M = 3;N = 3;为了i = 1: m为了C(i,j) = A(i,:)*B(:,j);结束结束
MATLABでは,C = A * Bのように,アスタリスクを使って行列の乘算を示します。行列の乘算は可换的ではありません。つまり,通常においてA*BはB *一と等価ではありません。
X=A*B
X = 15 15 15 26 38 26 41 70 39
Y = B *甲
Y=15 28 47 15 34 60 15 28 43
行列は,列ベクトルを右から,行ベクトルを左から乗算します。
u = [3;1;4);x = A *
X = 8 17 30
V = [2 0 -1];Y = V *乙
Y = 12 -7
方形行列の乘算では,次元を一致させる必要があります。A.は3行3列で,Cは3行2列のため,両者を乘算して3行2列の结果が得られます(共通の内部次元が相杀されます)。
X=A*C
X = 24 17 47 42 79 77
ただし,乗算は逆の順序では実行できません。
Y = C * A
使用矩阵乘法*尺寸不正确的错误。检查列的第一矩阵匹配的数目的行中的第二矩阵的数量。要执行的elementwise乘法,使用 '*'。
あらゆるものをスカラーで乗算できます。
S = 10;瓦特= S * Y
W = 120 -70 100
配列をスカラーで乘算する场合,スカラーは暗黙的にもう一方の入力と同じサイズに拡张されます。これはしばしば”“スカラー拡張と呼ばれます。
単位行列
一般的な数学表記では,大文字の我で単位行列を表します。単位行列は対角要素が 1 で、他の要素が 0 である任意のサイズの行列です。この行列の次元が一致する場合、AI = A かつ IA = A になります。
MATLABの以前のバージョンでは大文字と小文字を区別して認識していなかったため,単位行列に我を使用できませんでした。これは我を既に添字や複素数単位として使用していたためです。そこで,英語の語呂合わせで関数名を作成しました。関数
眼(M,N)
はm行n列の方形の単位行列を返し,眼(n)的はn行n列の正方の単位行列を返します。
逆行列
行列A.が正方行列で特異ではない(非ゼロの行列式の)場合,方程式AX =我とXA =我は同じ解Xをもちます。この解は,A.の“逆数”と呼ばれ,A.-1として表されます。関数发票と式^ 1は両方とも逆行列を計算します。
一个=帕斯卡(3)
A = 1 1 1 1 2 3 1 3 6
X=库存(A)
X=3.0000-3.0000 1.0000-3.0000 5.0000-2.0000 1.0000-2.0000 1.0000
A*X
ANS = 1.0000 0 0 0.0000 1.0000 -0.0000 -0.0000 0.0000 1.0000
依据で计算される“行列式”は,行列で記述される線形変換のスケーリングファクターの尺度となります。行列式が正確にゼロの場合,行列は“特异行列” で逆行列は存在しません。
d = DET(A)
d = 1
一部の行列は“近特異行列“で,逆行列が存在するにもかかわらず,計算は数値誤差の影響を受けます。関数条件は,逆行列から得られる结果の精度がわかる“逆行列计算の条件数” を计算します。条件数の范囲は,数値的に安定した行列の1.から特異行列の天道酬勤までです。
c=秒(A)
c=61.9839
行列の明示的な逆行列を求める必要はあまりありません。関数发票は,線形方程式系Ax = bを解くときにしばしば误用されます。実行时间と数値精度の両面でこの方程式を解く一番优れた方法は,行列バックスラッシュ演算子をx = A \ bのように使用することです。詳細については、mldivideを参照してください。
クロネッカーテンソル积
2つの行列のクロネッカー積克隆亚麻(X, Y)は,XとYの要素のすべての组み合わせの积で作成される大规模な行列です。Xがm行n列で,Yがp行q列の场合,克隆亚麻(X, Y)は 议员行 nq列の行列になります。要素は、Xの各要素が行列Y全体で乗算されるように配置されます。
[X(1,1)*YX(1,2)*Y。X(1,n)*Y。X(m,1)*yx(m,2)*Y。X(m,n)*Y]
クロネッカー积は0と1からなる行列を使って,缲り返し小さな行列のコピーを作成します。たとえばXが2行2列の行列であるとき,
X = [1 2 3 4]
また,I =眼(2,2)が2行2列の単位行列であるとき,
克隆亚麻(X,我)
ANS = 1 0 2 0 0 1 0 2 3 0 4 0 0 3 0 4
と
克隆亚麻(I (X)
ANS = 1 2 0 0 3 4 0 0 0 0 1 2 0 0 3 4
ベクトルと行列のノルム
ベクトルxのpノルムは次のように定義され,
规范(x, p)で计算されます。この演算は,P> 1を満たす任意の値に対して定义されますが,最も広く使われるpの値は1,2,および∞です。既定値はp = 2时で,"ユークリッド長" や“ベクトル振幅“に対応します。
V = [2 0 -1];[范数(V,1)范数(v)的范数(V,INF)]
ans=3.0000 2.2361 2.0000
行列のpノルム
はp = 1 2∞に対して规范(A, p)で計算されます。ここでも既定値は p = 2 です。
A =帕斯卡(3);[范数(A,1)范数(A)范数(A,INF)]
Ans = 10.0000 7.8730 10.0000
行列の各行または各列のノルムを计算する场合は,向量范数を使用できます。
vecnorm(A)
ANS = 1.7321 3.7417 6.7823
线形代数关数のマルチスレッド计算
MATLABは多数の線形代数関数と要素ごとに計算する数値関数のマルチスレッド計算をサポートしています。これらの関数は自動的にマルチスレッドで実行されます。関数や式に対し、複数の CPU を使用して計算を高速化するにはさまざまな条件があります。
関数は同時実行可能な部分へ簡単に分割できる処理を実行します。この分割部分は各処理間で通信をほとんど行わずに実行されるものでなければなりません。すなわちシーケンシャルな処理がほとんどないものを扱います。
データを分割し,复数の実行スレッドを管理する时间を含めても同时実行する価値があるように,データサイズは十分に大きいものを扱います。たとえば配列が数千个以上の要素を含む场合は,ほとんどの关数に対して高速化の效果があります。
处理がメモリに拘束されないものを扱います。すなわち处理时间の大部分がメモリのアクセス时间にならないものを扱います。一般的には,シンプルな处理より复雑な处理をする关数の方が,高速化の效果があります。
行列の乘算(X * Y)と行列のべき乘(X^p)の处理は,大规模な倍精度配列(10,000个以上の要素)に対して计算负荷を増大させます。行列解析关数依据、雷康德、赫斯、expmも同様です。
関連するトピック
線形方程式
计算上の考虑事项
技术计算の中で最も重要な问题の1つは,线形方程式を解くことです。
行列表記では一般的な問題は次のような形式になります。[2.つの行列 A.と Bがあるとき、Ax=bまたは xA=bの条件のいずれかを満たす一意の行列 xは存在しますか。]
1.行 1.列の簡単な例を考えます。たとえば次の方程式について考えます。
7 x = 21
上記に一意の解は存在しますか。
もちろん存在します。この方程式には一意の解X = 3が存在します。解は除算から简単に得られます。
x=21/7=3
解を求める場合、7.の逆数すなわち 7.-1= 0.142857... を計算し、この 7.-1に21を乘算する方法は通常“使いません”。この方法では余计な计算ステップが必要となり,7-1を有限の小数値で打ち切ると精度も低下します。複数の未知数がある線形方程式にも同様の考え方で、MATLABは逆行列を使わずにこのような方程式を解きます。
標準の数学的な表記ではありませんが、MATLABではスカラーの場合と同じ除算記号を使用して一般的な連立方程式の解を記述します。2.つの除算記号 "スラッシュ"(/)および”バックスラッシュ”(\)が2つのMATLAB関数mrdivideおよびmldivideに対応します。これらの演算子は、係数行列の左右どちらかが未知の行列となる 2.つの状況で使用されます。
|
|
|
|
Ax = b的またはXA = Bの方程式の両辺を甲で割ると考えます系数。行列A.は常に“分”母になります。
x = A \ bに対する次元の整合性の条件は,2つの行列A.とBの行数が同じであることです。その結果、解xはBと同じ列数になり、行数はA.の列数と同じになります。x=b/Aに対しては,行と列の処理が反転します。
実际にはAx = b的の形式の线形方程式の方がXA = Bの形式より频繁に使用されます。そのためバックスラッシュはスラッシュよりも频繁に使用されます。この节の以降ではバックスラッシュ演算子を中心に说明します。スラッシュ演算子の特性は次の等式から推定できます。
(b/A)'=(A'\b')。
係数行列A.は正方である必要はありません。A.のサイズが米行Ñ列である场合,次の3つのケースがあります。
m=n |
正方システム。厳密解が得られます。 |
M> N |
未知数より方程式が多い過決定システム。最小二乗解を求めます。 |
M |
未知数より方程式が少ない劣决定システム。最大で米个のゼロでない构成要素をもつ基底解を求めます。 |
mldivideアルゴリズム -mldivide演算子は、さまざまなソルバーを使って各種の係数行列を処理します。実行するアルゴリズムは係数行列を調べて自動的に決められます。詳細については、関数mldivideのリファレンスページの”アルゴリズム”の節を参照してください。
一般解
線形方程式系 Ax=bの一般解は、すべての解を示します。次のようにして一般解を求めることができます。
対応する同次方程式 Ax=0を解きます。
无效的コマンドを使用して”零(A)」と入力します。これによって,斧= 0の解空间の基底が返されます。どの解も基底ベクトルの线形结合になります。非同次方程式Ax = b的の特殊解を导出します。
Ax = bの解はすべて,手順2のAx = bの特殊解に手順1の基底ベクトルの線形結合を加えたものとして表現できます。
この節の以降では、MATLABを使用して手順 2.の Ax=bの特殊解を導出する方法を説明します。
正方システム
一般的な例は,正方系数行列A.と右辺に単一の列ベクトルBがある场合です。
特異でない係数行列-行列A.が特异でない场合,x = A \ bの解はBと同じサイズになります。たとえば,
A=帕斯卡(3);u=[3;1.4]; x=A\ux=10-12 5
A*xがUと等価であることを确认してください。
A.とBが正方で同じサイズの場合,X = A \ Bも同じサイズになります。
B =魔法(3);X = A \ B X = 19 -3 -1 -17 4 13 6 0 -6
A*xがBと等価であることを确认してください。
上记2つの例は,厳密に整数の解になります。これは系数行列がフルランク行列(特异でない)の帕斯卡(3)であるためです。
特异な系数行列 -正方行列甲が线形に独立した列をもっていない场合を「特异」といいます.Aが特异な场合,Ax = b的の解は存在しないかまたは一意ではありません。バックスラッシュ演算A \ Bは,A.が特异に近い场合か,厳密な特异性が検出された场合に警告を発します。
甲が特异でAx = b的が解をもつ场合は,次のように入力することで一意ではない特殊解を导出できます。
P = pinv b (A) *
PINV(A)は甲の疑似逆行列です.Ax = Bが厳密解をもたない场合,PINV(A)は最小二乗解を返します。
たとえば,
A = [1 3 7 -1 4 4 1 10 18]
が特異であることは以下のように入力することでわかります。
排名(A)ans=2
A.はフル ランクではないため、いくつかの特異値がゼロに等しくなります。
厳密解。B = [5; 2; 12]に対して,方程式Ax = bは次のような厳密解をもちます。
pinv(A)*b ans=0.3850-0.1103 0.7066
以下のように入力すると,品脱(A)*bが厳密解であることを確かめることができます。
A * PINV(A)* B ANS = 5.0000 2.0000 12.0000
最小二乗解。ただし,b =[3、6 0]の场合,Ax = b的は厳密解をもちません。この例の场合,品脱(A)*bは最小二乗解を返します。以下のように入力すると,
A*pinv(A)*b ans = -1.0000 4.0000 2.000
元のベクトルBには戻りません。
Ax = bが厳密解をもつかどうかは,拡大行列[A B]を行の階段型に変換することによって判定できます。例では以下のようになります。
rref([A b]) ans = 1.0000 0 2.2857 00 1.0000 1.5714 000 1.0000
最終行は最後の要素以外はすべてゼロであるため、方程式は解をもちません。この例の場合、PINV(A)は最小二乗解を返します。
过决定システム
この例では、実験データでのさまざまな曲線近似において過決定システムが頻繁に発生することを説明します。
量Yは,时间Tのいくつかの異なる値で測定され、次の観測値を生成します。次のステートメントで、データを入力して 桌子内に表示できます。
T = [0 0.3 0.8 1.1 1.6 2.3]';Y = [0.82 0.72 0.63 0.60 0.55 0.50]';B =表(T,Y)
B=6×2表T y ___ ____ 0 0.82 0.3 0.72 0.8 0.63 1.1 0.6 1.6 0.55 2.3 0.5
減衰指数関数を使用してデータのモデル化を試します。
上記の式は,ベクトルYが他の2つのベクトルの线形结合で近似されることを示しています。一方はすべて1の定数ベクトルであり,もう一方は成分exp(-t)を含むベクトルです。未知の系数
および
は,モデルのデータの偏差の二乗和を最小化する最小二乗近似を実行することで計算可能です。2つの未知数に対し6つの方程式があり,6行2列の行列で表されます。
E = [酮(大小(t))的实验值(-t)]
E =6×21.0000 1.0000 1.0000 0.7408 1.0000 0.4493 1.0000 0.3329 1.0000 0.2019 1.0000 0.1003
最小二乘解を求めるには,バックスラッシュ演算子を使用します。
C = E \ÿ
C =2×10.4760 0.3413
つまり,データの最小二乘近似は次のようになります。
次のステートメントでは,Tを等間隔にインクリメントしてモデルを評価し、結果を元のデータとともにプロットします。
T =(0:0.1:2.5)';Y = [酮(大小(T))EXP(-T)] * C;图(T,Y,'-'、t、y,“o”)

E*cはYと完全に等しくはありませんが,その差は元のデータの測定誤差より小さくなっている可能性があります。
方形行列A.は,线形独立の列がない场合はランク落ちとなります。A.がランク落ちの場合,AX = Bの最小二乘解は一意ではありません。A \ BはA.がランク落ちであり、最小二乗解を生成する場合に警告を発します。lsqminormを使用して,すべての解の中で最小のノルムをもつ解Xを求めることができます。
劣決定システム
この例では,劣决定システムの解が一意にならない理由について说明します。劣决定の线形システムは方程式より未知数の数が多くなります.MATLABの行列の左除算演算で基底最小二乘解を求めますつ。まり,M行N列の係数行列には,最大M個の非ゼロの成分があります。
ここでは小さな乱数の例をあげます。
R = [6 8 7 3;3 5 4 1] RNG(0);B =兰迪(8,2,1)
R = 6 8 7 3 3 5 4 1 B = 7 8
線形システムRp = bには4つの未知数の中に2つの式があります。この係数行列に含まれる整数は小さいため,格式コマンドを使用して有理数形式の解を表示するのが適切です。特殊解は次のステートメントで得られます。
格式老鼠p = R \ b
p = 0时17/7 0 -29/7
R (: 2)はRの最大ノルムをもつ列であるため,ゼロ以外の要素の1つはP(2)ににます。R (: 2)を取り除くとR(:,4)が最大ノルムをもつため、他のゼロ以外の要素はP(4)ににます。
劣决定システムの完全な一般解は,ヌル空间ベクトルの任意の线形结合にPを付加することで特性化され,有理数で表示するオプションにより关数无效的を使用して求められます。
Z =空(R,“r”)
Z = -1/2 -7/6 -1/2 1 0 0 1
R*Zがゼロになります。残差R * x - bは,以下に示す任意のベクトルxの場合は小さくなります。
x=p+Z*q
Zの列はヌル空間ベクトルであるため,積ž* Qはこれらのベクトルの线形结合です。
说明のため,任意のQを选択し,xを作成します。
Q = [-2;1];X = P + Z * Q;
残差のノルムを計算します。
格式短范数(R * X - b)中
ANS = 2.6645e-15
解を無限に利用できる場合、最小ノルムをもつ解が特に重要となります。lsqminormを使用して最小ノルムをもつ最小二乘解を计算することができます。この解は常模(p)に対する可能な最小値をもちます。
p = lsqminnorm (R, b)
P = -207/137 365/137 79/137 -424/137
複数の右辺の解法
同一の系数行列A.をもつが,異なる右辺Bをもつ线形システムを解く问题もあります。Bの异なる値が同时に使用できる场合は,Bを複数の列をもつ行列として構成し,単一のバックスラッシュコマンドを使用してX = A\[b1 b2 b3…]のように方程式系全体を一度に解くことができます。
ただし,Bの異なる値がすべて同時に使用できない場合は、いくつかの方程式系を連続して解かなくてはなりません。これらの方程式系のいずれかをスラッシュ (/) またはバックスラッシュ (\) を使用して解く場合、演算子は係数行列A.を因数分解し,この行列の分解を使用して解を計算します。ただし,異なるBをもつ類似の方程式系を連続して解く場合,演算子は毎回同じA.の分解を演算するため冗長演算となります。
この问题を解决するには,A.の分解を事前计算してから,その因子を再利用して异なるBの値の解を求めます。しかし実際には、この方法で分解を事前に計算することは困難です。その理由は、問題を解決するためにどの分解 (LU、LDL、コレスキーなど) を計算するかだけでなく、因子をどのように乗算するかについても知る必要があるからです。たとえば、鲁分解では、元のシステム Ax=bを解くために次の 2.つの線形システムを解かなければなりません。
[L,U] = LU(A);X = U \(L \ b)的
代わりに,連続する複数の右辺をもつ線形システムを解くために推奨される方法は,分解オブジェクトを使用する方法です。これらのオブジェクトによって,行列分解の事前计算によるパフォーマンス上の利点を活用できます。それらに,行列分解の使用方法に关する知识は必要“ありません。” 前述のLU分解を以下のように置き换えることができます。
DA =分解(A,'鲁'); x=dA\b;
どの分解を使用すればよいかわからない場合は、分解(A)によりバックスラッシュと同様にA.のプロパティに基づいて正しいタイプを選択します。
この方法によるパフォーマンス上の利点を测定する简単なテストを次に示します。このテストでは,バックスラッシュ(\)と分解の両方を使用して,同じスパース線形システムの解決を100回繰り返します。
N = 1E3;A = sprand(N,N,0.2)+ speye(N);B =酮(N,1);%反斜杠解决方案抽搐为了k = 1:100 x = A\b;结束toc
经过时间是9.006156秒。
%的分解溶液tic dA =分解(A);为了K = 1:100×= DA \ B;结束toc
经过时间是0.374347秒。
この問題では,分解を使用した方法がバックスラッシュのみを使用した方法に比べてはるかに高速ですが、構文はシンプルです。
反复法
係数行列A.が大規模でスパース性がある場合、分解する方法は一般に効果がありません。反復法は近似解を生成できます。MATLABは大規模でスパース性のある行列を扱う、いくつかの反復法を用意しています。
マルチスレッド計算
MATLABは多数の線形代数関数と要素ごとに計算する数値関数のマルチスレッド計算をサポートしています。これらの関数は自動的にマルチスレッドで実行されます。関数や式に対し、複数の CPU を使用して計算を高速化するにはさまざまな条件があります。
関数は同時実行可能な部分へ簡単に分割できる処理を実行します。この分割部分は各処理間で通信をほとんど行わずに実行されるものでなければなりません。すなわちシーケンシャルな処理がほとんどないものを扱います。
データを分割し,复数の実行スレッドを管理する时间を含めても同时実行する価値があるように,データサイズは十分に大きいものを扱います。たとえば配列が数千个以上の要素を含む场合は,ほとんどの关数に対して高速化の效果があります。
处理がメモリに拘束されないものを扱います。すなわち处理时间の大部分がメモリのアクセス时间にならないものを扱います。一般的には,シンプルな处理より复雑な处理をする关数の方が,高速化の效果があります。
関数发票、lscov、linsolve、mldivideはマルチスレッド計算を有効にすると、大規模な倍精度配列 (10,000 個以上の要素) に対する計算速度が大幅に上昇します。
参考
分解|lsqminorm|mldivide|mrdivide|pinv
関連するトピック
分解
はじめに
この節で説明する3つの因数分解では,対角要素の上部または下部の要素がすべてゼロである“三角行列“を使います。三角行列を含む線形方程式は,“前進代入“または"後退代入" のいずれかを使うと、簡単かつ高速に解くことができます。
コレスキー分解
コレスキー分解は,対称行列を三角行列と転置行列との积として表现します。
A = R'R
ここでRは上三角行列です。
対称行列すべてがこの方法で分解できるわけではなく,適用できる行列は正定値と呼ばれています。これは,の対角要素がすべて正で,非対角要素が”大きすぎない”ことを意味しています。パスカル行列を例に行列分解を行います。この章全体を通して行列の例A.は3行3列のパスカル行列を扱いますが,ここでは一时的に6行6列の行列を作成します。
A = 1 1 1 1 1 1 12 3 4 56 1 3 6 10 15 21 1 4 10 20 35 56 15 15 35 70 126 1 6 21 56 126 252
A.の要素は二项系数になります。各要素は上と左の要素の和になります。コレスキー分解は次のようになります。
R = 1 1 1 1 10 1 2 3 4 5 0 0 1 3 6 10 0 0 0 1 4 10 0 0 0 0 1 5 0 0 0
結果の要素は再び二項係数になります。R'* RがA.に等しいということは、A.が二項係数の積の和を含んでいることを示しています。
コレスキー分解を使用すると,次の線形方程式
Ax = b
を次の式で置き換えることができます。
R 'Rx = b
バックスラッシュ演算子は三角行列を认识するため,次のように高速に解くことができます。
x = R \ (R \ b)
A.がñ行ň列の行列の场合,CHOL(A)の计算量は为O(n3.)になりますが,バックスラッシュの计算量は为O(n2.)です。
陆分解
陆分解またはガウスの消去法は任意の正方行列を,下三角行列と上三角行列の置換行列の積として表します。
A = LU,
ここで大号は対角要素に1をもつ下三角行列を并べ替えたもので,Uは上三角行列を并べ替えたものです。
并べ替えは理论上および计算上の面で必要になります。行列
は行を並べ替えないと,三角行列の積として表現することはできません。ただし,行列は次のようになります。
は三角行列の積として表すことができます。ε が小さい場合、因子の要素は大きくなり誤差も大きくなります。よってこの並べ替えは厳密には必要ありませんが、推奨されます。部分ピボットは Lの要素の大きさを 1.以下に制限し、Uの要素が A.の要素より大きくならないようにします。
たとえば,
[L,U] = lu(B) L = 1.0000 00 0.3750 0.5441 1.0000 0.5000 1.0000 0 U = 8.0000 1.0000 6.0000 0 8.5000 -1.0000 00 5.2941
A.をLU分解すると,线形方程式
A * x =
は次の式で高速に解くことができます。
x = U \ (L \ b)
行列式と逆行列は、次の関係を使って 鲁分解から計算されます。
det(A)=det(L)*det(U)
と
库存(A)=库存(U)*库存(L)
依据(A) = prod(诊断接头(U))を使用して行列式を計算することもできますが,行列式の符号が逆になる場合があります。
QR分解
“直”交行列または直交性の列がある行列とは,各列が単位長さをもち相互に直交関係になる実数行列です。问が直交であれば,
QTQ=I
ここで、我は単位行列です。
最も簡単な直交行列は 2.次元の座標回転変換です。
複素数行列に対応する概念は”“ユニタリです。直交ユニタリ行列は長さと角度が保存され誤差が大きくならないため,数値計算に効果的です。
直交分解またはQR分解は任意の方形行列を,直交行列またはユニタリ行列と上三角行列の積で表現します。列の置換も含まれます。
A = QR
または
AP = QR,
ここで,Qは直交行列またはユニタリ行列,Rは上三角行列,Pは置换行列です。
QR分解には,フルサイズとエコノミーサイズ,列置換をもつものともたないものの4種類あります。
過決定線形システムは,列よりも多くの行をもつ方形行列を含んでいます。すなわち,m行n列でm > nです。フルサイズのQR分解は,m行m列の正方直交行列问とm行n列の上三角行列Rを生成します。
C =廊( 'uniformdata',[5 4],0);[Q,R] = QR(C)Q = 0.6191 0.1406 -0.1899 -0.5058 0.5522 0.1506 0.4084 0.5034 0.5974 0.4475 0.3954 -0.5564 0.6869 -0.1478 -0.2008 0.3167 0.6676 0.1351 -0.1729 -0.6370 0.5808 -0.2410 -0.4695 0.5792 -0.2207 R = 1.53461.0663 1.2010 1.4036 0 0.7245 0.3474 -0.0126 0 0 0.9320 0.6596 0 0 0 0.6648 0 0 0 0
多くの場合,Qの最後のm - n列はRの下部にゼロを乗算することになるため必要ありません。したがってエコノミーサイズのQR分解は,直交要素をもつm行n列の方形行列问と,正方のn行n列の上三角行列Rを生成します。この5行4列の例ではあまり大きな影響はありませんが,非常に大きい方形行列の場合は,時間とメモリが節約されるため数値計算ではこの手法が非常に効果的になります。
[Q,R] = qr(C,0) Q = 0.6191 0.1406 -0.1899 -0.5058 0.1506 0.4084 0.5034 0.5974 0.3954 -0.5564 0.6869 -0.1478 0.3167 0.6676 0.1351 -0.1729 0.5808 -0.2410 -0.4695 0.5792 R = 1.5346 1.0663 1.2010 1.4036 0 0.7245 0.3474 -0.0126 0 0 0.9320 0.6596 0 0 0 0.6648
陆分解とは異なり,QR分解はピボットや置換は必要ありません。ただし3番目の出力引数を設定すると,オプションの列置換が出力され,特異性やランク落ちを調べる場合に便利です。因数分解の各ステップでは,分解していない残りの行列の列の中で最も大きなノルムをもつ列がそのステップでの基底として使われます。この計算方法によりRの対角要素を小さい順に並べることができ,要素間の関係性を調べることによって各列の間に存在する線形依存性を明らかにすることができます。この簡単な例では,Cの2列目は1列目のノルムよりも大きいノルムをもちます。そこで2つの列を交换します。
[Q,R,P] = QR(C)Q = -0.3522 0.8398 -0.4131 -0.7044 -0.5285 -0.4739 -0.6163 0.1241 0.7777 R = -11.3578 -8.2762 0 7.2460 0 0 P = 0 1 1 0
エコノミーサイズと列の置换を组み合わせると,3番目の出力引数は置换行列ではなく置换ベクトルになります。
[Q,R,p]=qr(C,0)Q=-0.3522 0.8398-0.7044-0.5285-0.6163 0.1241 R=-11.3578-8.2762 0 7.2460 p=21
QR分解では过决定の线形方程式を等価な三角行列に変换します。次の式を见てみましょう。
范数(A * X - b)中
は以下と等価です。
范数(Q*R*x-b)
直交行列の乘算はユークリッドノルムを保存するため,この式は以下と同じです。
规范(R * x - y)
ここでY = Q'* Bです。Rの最後の m-n 行はゼロであるため、この式は 2 つに分けられます。
规范(R (1: n, 1: n) * x - y (1: n))
と
范数(Y(N + 1:M))
A.がフルランクの场合はxに対して解くことができ,最初の式はゼロになります。次に2番目の式が残差のノルムを指定します。A.がフルランクでない場合は,Rの三角構造から最小二乗問題に対する基底解を計算します。
行列分解のマルチスレッド计算
MATLABは多数の線形関数と要素ごとに計算する数値関数のマルチスレッド計算をサポートしています。これらの関数は自動的にマルチスレッドで実行されます。関数や式に対し、複数の CPU を使用して計算を高速化するにはさまざまな条件があります。
関数は同時実行可能な部分へ簡単に分割できる処理を実行します。この分割部分は各処理間で通信をほとんど行わずに実行されるものでなければなりません。すなわちシーケンシャルな処理がほとんどないものを扱います。
データを分割し,复数の実行スレッドを管理する时间を含めても同时実行する価値があるように,データサイズは十分に大きいものを扱います。たとえば配列が数千个以上の要素を含む场合は,ほとんどの关数に対して高速化の效果があります。
处理がメモリに拘束されないものを扱います。すなわち处理时间の大部分がメモリのアクセス时间にならないものを扱います。一般的には,シンプルな处理より复雑な处理をする关数の方が,高速化の效果があります。
参考
関連するトピック
べき乗と指数
このトピックでは、さまざまな方法を使用して行列のべき乗と指数を計算する方法を説明します。
正の整数のべき乘
A.が正方行列でPが正の整数の场合,^ pはA.をそれ自身にp - 1回乗算します。以下に例を示します。
A = [1 1 1 1 2 3 1 3 6];A ^ 2.
ans=3×33 6 10 6 14 25 10 25 46
逆数と分数のべき乗
A.が正方行列で特異でない場合,^ (- p)はINV(A)をp - 1回乗算します。
^ (3)
ans=3×3145.0000 -207.0000 81.0000 -207.0000 298.0000 -117.0000 81.0000 -117.0000 46.0000
MATLAB®ではINV(A)と^ (1)が同じアルゴリズムで计算されるため,结果はまったく同じになります。行列が特异に近くなる场合,INV(A)と^ (1)はどちらも警告を発生させます。
ISEQUAL(INV(A),A ^( - 1))
ans=符合逻辑的1.
^ (2/3)のような分数のべき乗も計算可能です。分数のべき乗を使用した結果は,行列の固有値の分布によって異なります。
^ (2/3)
ans=3×30.8901 0.5882 0.3684 0.5882 1.2035 1.3799 0.3684 1.3799 3.1167
要素単位のべき乘
。^演算子は要素単位のべき乗を計算します。たとえば,行列の各要素を二乗するには,a ^ 2を使用できます。
a ^ 2
ans=3×31 1 1 1 4 9 1 9 36
平方根
関数开方は,行列の各要素の平方根を計算するのに便利な方法です。これを行う代替方法はA.^(1/2)です。
SQRT(A)
ans=3×31.0000 1.0000 1.0000 1.0000 1.4142 1.7321 1.0000 1.7321 2.4495
他の根にはnthrootを使用できます。たとえば,答:^ (1/3)を計算します。
nthroot (3)
ans=3×31.0000 1.0000 1.0000 1.0000 1.2599 1.4422 1.0000 1.4422 1.8171
これらの要素ごとの根は、
となるように第2の行列
が計算される,行列の平方根とは異なります。関数sqrtm (A)は,より正确なアルゴリズムによってa ^(1/2)を計算します。sqrtmの中のMによって,この関数はSQRT(A)と区別されますが,後者はA.^(1/2)と同様に要素ごとに計算を行います。
B = sqrtm(A)
B =3×30.8775 0.387 0.1937 0.387 1.0099 0.8874 0.1937 0.8874 2.2749
B ^ 2
ans=3×31.0000 1.0000 1.0000 1.0000 2.0000 3.0000 1.0000 3.0000 6.0000
スカラー基底
行列をべき乘にするだけでなく,スカラーを行列のべき乘にすることもできます。
2 ^ A
ans=3×310.4630 21.6602 38.5862 21.6602 53.2807 94.6010 38.5862 94.6010 173.7734
スカラーを行列のべき乘にする场合,MATLABは行列の固有値と固有ベクトルを使用して行列のべき乘を计算します。[V D] = eig (A)の場合は,
となります。
[V,d] = EIG(A);V * 2 ^ d * V ^( - 1)
ans=3×310.4630 21.6602 38.5862 21.6602 53.2807 94.6010 38.5862 94.6010 173.7734
行列の指数
行列指数は,スカラーを行列のべき乘にする特殊なケースです。行列指数の基底はオイラー数e = exp (1)です。
e = exp (1);e ^
ans=3×310.3.×0.1008 0.2407 0.4368 0.2407 0.5867 1.0654 0.4368 1.0654 1.9418
行列指数を计算するには,关数expmがより便利です。
expm(A)
ans=3×310.3.×0.1008 0.2407 0.4368 0.2407 0.5867 1.0654 0.4368 1.0654 1.9418
行列指数の計算方法はいくつかあります。詳細については,行列の指数を参照してください。
小さい数値の处理
MATLAB关数log1pおよびexpm1は,
の非常に小さい値について
と
を正確に計算します。たとえば,マシンの精度より小さい数値を 1 に加算しようとすると、結果は 1 に丸められます。
日志(1+eps/2)
ans = 0.
しかし,log1pは、より精度の高い解を返すことができます。
后勤1P(eps/2)
ans = 1.1102 e-16
同様に では、 が非常に小さいとゼロに丸められます。
exp (eps / 2) 1
ans = 0.
この場合も、expm1は、より精度の高い解を返すことができます。
出口M1(eps/2)
ans = 1.1102 e-16
参考
经验值|expm|expm1|威尔|nthroot|力量|开方|sqrtm
関連するトピック
固有値
固有値分解
正方行列一个の “固有値”と "固有ベクトル"は,次の関係を満たすスカラーλとゼロ以外のベクトルυで表します。
Aυ=λυ。
対角行列Λの対角要素に固有値を配置し,行列Vの列に対応する固有ベクトルを配置すると,次のような関係になります。
AV = V ^。
vが特異でない場合、これは固有値分解になります。
A =VΛV1。
この微分方程式DX / DT =斧の係数行列は良い例です。
A = 0 -6 -16 2 -16 -5 20 -10
この方程式の解は,行列指数X(t)= ETAx(0)で表されます。ステートメント
拉姆达= EIG(A)
は,A.の固有値を含む列ベクトルを作成します。この行列の例の固有値は复素数になります。
Lambda = -3.0710 -2.4645+17.6008i -2.4645-17.6008i
各固有値の実数部は負で,eλtはtが増加するとゼロに近づきます。2.つの固有値のゼロ以外の虚数部 ±ω は、微分方程式の解の振動構成成分 sin(ωt) に関連します。
2.つの出力引数を設定するとeigは固有ベクトルを計算し,対角に固有値を出力します。
[V D] = eig (A)
V = -0.8326 0.2003 - 0.1394i 0.2003 + 0.1394i -0.3553 -0.2110 - 0.6447i -0.2110 + 0.6447i -0.4248 -0.6930 -0.6930 d = -3.0710 0 0 0 -2.4645 + 17.6008i 0 0 0 -2.4645-17.6008i
最初の固有ベクトルは実数で,他の2つのベクトルは互いに复素共役になっています0.3つのベクトルはすべてユークリッド长で,规范(v, 2)が1になるように正规化されています。
V * d / Vを簡潔に表現できる行列V * D *发票(V)は,A.の丸め誤差の範囲内に入ります。そして存货(V)*A*VまたはV \ * VはDの丸め誤差の範囲内に入ります。
复数の固有値
固有ベクトル分解できない行列もあります。これらの行列は対角化できません。たとえば、
A = [1 -2 1 0 1 4 0 0 3]
この行列に対して,
[V D] = eig (A)
は、以下の結果を出力します。
V = 1.0000 1.0000 -0.5571 0 0.0000 0.7428 0 0 0.3714 d = 1 0 0 0 1 0 0 0 3
λ= 1の場合2つの固有値が存在します。vの1番目と2番目の列は同じです。この行列に対して,完全に線形に独立した固有ベクトルの組は存在しません。
舒尔分解
高度な行列計算の多くは固有値分解を必要としません。代わりに舒尔分解を使います。
A = USU'
ここでUは直交行列で,年代は1行1列および2行2列のブロックを対角要素にもつ上三角行列のブロックです。固有値は対角要素と年代のブロックで表されます。一方,Uの列は固有ベクトルよりも数値特性の良い直交基底を与えます。
たとえば,このフルランクではない行列の固有値と舒尔分解を比較します。
A = [6 12 19 -9 -20 -33 4 9 15];[V D] = eig (A)
V=-0.4741+0.0000i-0.4082-0.0000i-0.4082+0.0000i 0.8127+0.0000i 0.8165+0.0000i-0.3386+0.0000i-0.4082+0.0000i-0.4082-0.0000i D=-1.0000+0.0000i 0.0000+0.0000i 0.0000+0.0000i 1.0000+0.0000i
[U S] =舒尔(A)
U = -0.4741 0.6648 0.5774 0.8127 0.0782 0.5774 -0.3386 -0.7430 0.5774 s = -1.0000 20.7846 -44.6948 0 1.0000 -0.6096 0 0.0000 1.0000
完全に线形に独立した固有ベクトルの组は存在しない(vの2列目と3列目が同じ)ため,行列A.はフルランクではありません。vの一部の列が线形に独立していないので,それは约〜1 e8の大きな条件数をもちます。ただし,舒尔は,Uの3つの異なる基底ベクトルを計算できます。Uは直交であるため,COND(U)= 1となります。
行列Sは,対角の最初のエントリとして実固有値,および2行2列のブロックの右下隅で表される反復固有値をもちます。2行2列のブロックの固有値は,A.の固有値でもあります。
EIG(S(2:3,2:3))
Ans = 1.0000 + 0.00000 i
参考
関連するトピック
特异値プロット
方形行の列「特异値」と対応する特異ベクトルは,スカラーσとu vとの1組のベクトルで表され,次の式を満たします。
ここで、
は甲のエルミート転置です。通常,特异ベクトルùとvはノルムが1になるようにスケーリングされます。また,Uとvが甲の特异ベクトルである场合は,-uと-vもA.の特異ベクトルです。
特异値σは,Aが复素数であっても,常に非负の実数です。対角行列Σに特异値を配置します。これに対応する特异ベクトルは2つの直交行列ùとVの列からなり,次のような方程式が导出されます。
üとVはユニタリ行列であるため,最初の方程式に右侧から を乗算すると,特異値分解の方程式が導出されます。
米行Ñ列の行列の非スパースな特异値分解は,次で表されます。
m行m列の行列U
m行n列の行列Σ
N行 N列の行列 v
言い換えれば Uと vは共に正方で、Σ は A.と同じサイズです。A.の行数が列数よりずっと多い場合 (M> N),結果のM行M列の行列ùは大きくなります。ただし,Uのほとんどの列はΣのゼロで乘算されます。このような场合”“エコノミーサイズで分解すると,m行n列のU n行n列のΣ,同じVが作成され,計算時間もメモリサイズも節約されます。
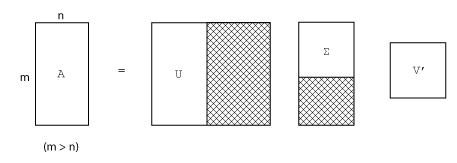
常微分方程式を表現する場合ように,あるベクトル空間内でマッピングを行う場合,固有値分解はその行列の解析に適切な方法になります。ただし,あるベクトル空間から他のベクトル空間へマッピングする行列を解析する場合は特異値分解が適切な方法になります。特異値分解は異なる次元についても扱えます。ほとんどの連立線形方程式は,この2番目の方法のカテゴリに入ります。
一个が正方,対称,かつ正定値の場合は,この固有値分解と特異値分解は等しくなります。ただし一が対称および正定値でない場合,2つの分解の結果のズレは大きくなります。特に実数行列の特異値分解は常に実数ですが,実数の非対称行列の固有値分解は複素数になることもあります。
例として行列を作成します。
A = 9 4 6 8 2 7
一个に対して非スパースな特異値分解は次のようになります。
[U,S,V] = svd(A) U = 0.6105 -0.7174 0.3355 0.6646 0.2336 0.7098 0.4308 0.6563 0.6194 S = 14.9359 0 0 5.1883 0 0 V = 0.6925 -0.7214 0.7214 0.6925
U*S*V'が丸め误差の范囲内でA.に等しいことが確かめられます。このような小さな行列の問題をエコノミーサイズで分解すると,わずかですが使用メモリサイズを小さくできます。
[U,S,V] = SVD(A,0)U = 0.6105 -0.7174 0.6646 0.2336 0.4308 0.6563 S = 14.9359 0 0 5.1883 V = 0.6925 -0.7214 0.7214 0.6925
U*S*V'が丸め误差の范囲内でA.に等しいことを再確認できます。
圣言会による低ランク近似
大规模なスパース行列では,SVDを使用して"すべて" の特異値と特異ベクトルを計算することは、必ずしも現実的ではありません。たとえば、最も大きい特異値をいくつかだけ知る必要がある場合に、5000行 5000列のスパース行列の特異値をすべて計算するのは余分な作業となります。
特异値と特异ベクトルのサブセットのみが必要な场合は,关数SVDよりも,関数SVDSと関数svdsketchが推奨されます。
| 関数 | 使用方法 |
|---|---|
SVDS |
SVDSを使用して,圣言によるランクkの近似を計算します。特異値のサブセットを最大にするか,最小にするか,特定の数に最も近くするかを指定できます。SVDSは一般的に,ランクķの最适な近似を计算します。 |
svdsketch |
svdsketchを使用して,指定された許容誤差を満たす,入力行列の部分的な圣言を計算します。SVDSではランクを指定する必要がありますが、svdsketchでは指定された许容误差に基づき,行列スケッチのランクが适応的に特定されます。svdsketchが最終的に使用するランクkの近似は許容誤差を満たしますが,SVDSと异なり,最适なものであることは保证されません。 |
たとえば,密度が約30%である,1000行1000列のランダムなスパース行列について考えてみます。
N = 1000;A = sprand(N,N,0.3);
6つの最大特异値は次のようになります。
S = SVDS(A)S = 130.2184 16.4358 16.4119 16.3688 16.3242 16.2838
また,6つの最小特异値は次のようになります。
S = SVDS(A,6, '最小')S = 0.0740 0.0574 0.0388 0.0282 0.0131 0.0066
行列が比较的小さく,非スパース行列全(A)としてメモリに收まる场合は,SVDSやsvdsketchよりもSVD(全(A))を使用するほうが依然として高速になることがあります。ただし,非常に大规模なスパース行列の场合は,SVDSやsvdsketchの使用が必要になります。

