Ziggurat随机法向发生器
这是关于MATLAB随机数发生器的多部分系列的第三部分。MATLAB使用George Marsaglia的ziggurat算法的变体来生成正态分布随机数已有近二十年的历史。
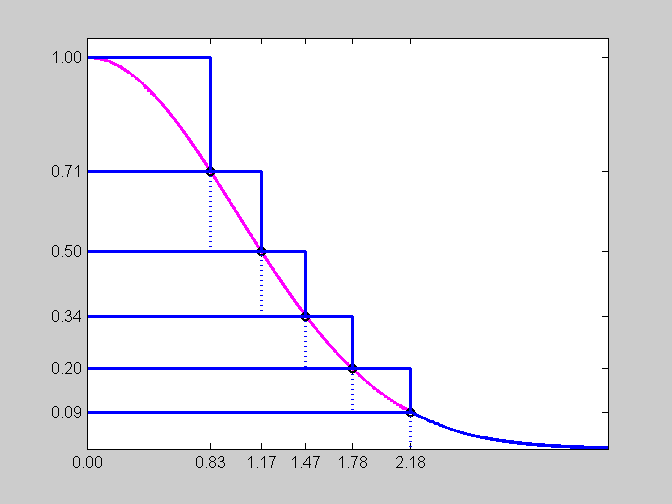 金字塔的顶部$n-1$部分是矩形。底部部分是一个矩形,在$f(x)$的图形下有一个无限的尾巴。矩形的右边位于图中用圆表示的点$z_k$处。f (z_1) = 1美元和美元f (z_ {n + 1}) = 0 $, $ k的高度th部分是美元(z_k) - f (z_ {k + 1})美元。关键思想是选择$z_k$,以便所有$n$的部分,包括底部的无界部分,具有相同的面积。还有其他算法用矩形来近似pdf下面的面积。Marsaglia算法的显著特征是,矩形是水平的,面积相等。
金字塔的顶部$n-1$部分是矩形。底部部分是一个矩形,在$f(x)$的图形下有一个无限的尾巴。矩形的右边位于图中用圆表示的点$z_k$处。f (z_1) = 1美元和美元f (z_ {n + 1}) = 0 $, $ k的高度th部分是美元(z_k) - f (z_ {k + 1})美元。关键思想是选择$z_k$,以便所有$n$的部分,包括底部的无界部分,具有相同的面积。还有其他算法用矩形来近似pdf下面的面积。Marsaglia算法的显著特征是,矩形是水平的,面积相等。
内容
梯形金字塔
为算法取一个容易记住的名字是很重要的。金字塔是古美索不达米亚的阶梯式神殿,从数学上讲,是二维阶梯函数。Marsaglia算法的基础是一个一维的金字巨轮。我不确定如果Marsaglia称它为“步进函数算法”,我们今天是否还会使用它。概率密度函数,或者pdf,正态分布的钟形曲线$$ f(x) = c e^{-x^2/2} $$,其中$c = 1/(2\pi)^{1/2}$是一个可以忽略的正态常数。如果我们要生成在平面上均匀分布的随机点$(x,y)$,并拒绝任何不属于这条曲线的点,剩下的$x$就形成了我们想要的正态分布。ziggurat算法用$n$ sections覆盖pdf下面略大的区域。下图有$n = 6$;我们今天使用的实际代码是n = 256。$n$的选择影响速度,但不影响代码的准确性。Z = zigplot(6)
Z = 0 0.8288 1.1713 1.4696 1.7819 2.1761
 金字塔的顶部$n-1$部分是矩形。底部部分是一个矩形,在$f(x)$的图形下有一个无限的尾巴。矩形的右边位于图中用圆表示的点$z_k$处。f (z_1) = 1美元和美元f (z_ {n + 1}) = 0 $, $ k的高度th部分是美元(z_k) - f (z_ {k + 1})美元。关键思想是选择$z_k$,以便所有$n$的部分,包括底部的无界部分,具有相同的面积。还有其他算法用矩形来近似pdf下面的面积。Marsaglia算法的显著特征是,矩形是水平的,面积相等。
金字塔的顶部$n-1$部分是矩形。底部部分是一个矩形,在$f(x)$的图形下有一个无限的尾巴。矩形的右边位于图中用圆表示的点$z_k$处。f (z_1) = 1美元和美元f (z_ {n + 1}) = 0 $, $ k的高度th部分是美元(z_k) - f (z_ {k + 1})美元。关键思想是选择$z_k$,以便所有$n$的部分,包括底部的无界部分,具有相同的面积。还有其他算法用矩形来近似pdf下面的面积。Marsaglia算法的显著特征是,矩形是水平的,面积相等。初始化
对于给定的截面数$n$,可以解一个超越方程来找到$z_n$,即无限尾部与最后一个矩形截面相交的点。在我们的$n = 6$的图片中,$z_n = 2.18$。在$n = 256$的实际代码中,$z_n = 3.6542$。一旦$z_n$已知,就很容易计算出section和其他右边端点$z_k$的公共面积。也可以计算$\sigma_k = z_{k-1}/z_k$,它是每个部分中位于上面部分下面的部分的分数。我们称这些分数部分为核心金字塔。核心的右边缘是图中的虚线。图$f(x)$所覆盖区域中虚线右侧的矩形的其余部分是提示.$z_k$ 's和$\sigma_k$ 's的计算只执行一次,并且这些值包含在源代码的头文件中。核心算法
通过这个初始化,正态分布随机数可以很快地计算出来。代码的关键部分计算一个随机整数$j$,在$1$和$n$之间,和一个均匀分布的随机数$u$,在$-1$和$1$之间。然后检查$u$是否落在$j$ th部分的核心。如果是这样,那么我们知道$u z_j$是pdf下点的$x$坐标,这个值可以作为正态分布的一个样本返回。代码看起来像这样。J = randi(256);U = 2*rand-1;如果abs(u) < sigma(j) r = u*z(j);Else r = tip_calculation end大多数$\sigma_j$的值都大于0.98,测试的正确率达到98.5%。一个正态随机数通常可以由一个随机整数、一个随机均匀数、一个if-test和一个乘法计算出来。由$j$和$u$决定的点落在尖端区域的概率小于1.5%。如果$j = 1$,因为顶部部分没有核心,如果$j$在$2$和$n-1$之间,随机点在其中一个尖端,或者如果$j = n$,点在无限尾巴中,就会发生这种情况。在这些情况下,需要更昂贵的小费计算。
精度
重要的是要认识到,即使金字型阶跃函数只近似于概率密度函数,得到的分布完全是正态分布。减少$n$会减少表所需的存储量,并增加所需额外计算的时间,但不会影响准确性。即使$n = 6$,我们也必须在25%的时间内进行更昂贵的修正,而不是小于1.5%,但我们仍然会得到精确的正态分布。变化
多年来,这一金字巨制的实施细节各不相同。Marsaglia和Tsang在1984年的原始论文中包含了一个相当复杂的处理提示的转换算法。我们在MATLAB的几个版本中使用了这个算法,我在程序中再现了它的行为randntx在MATLAB数值计算.这个方法和代码现在已经过时了。Marsaglia和Tsang在2000年发表的论文jstatsoft下面给出的链接有一个更简单的拒绝算法用于提示。我们已经在最近的MATLAB版本中使用了它,包括当前的版本。底层均匀发生器
Marsaglia和Tsang急于让他们的普通发电机和他们的制服发电机一样快。但他们有点太焦虑了。他们最初的代码只调用了一个32位的统一生成器。他们使用高阶7位作为垂直索引$j$,然后重用所有32位来获得水平横坐标$u$。后来的研究人员,包括Jurgen Doornik,发现这种相关性导致了某些统计测试的失败。我们现在对32位的Mersenne Twister生成器进行两次调用(在顺序计算期间)。我们用8位得到$j$,然后用剩下56位中的52位得到双倍精度$u$。这对时间有什么影响?分配一个长向量。清除m = 25e6 x = 0 (m,1);
M = 25000000生成一个随机均匀向量和一个随机法向量。然后比较两次执行时间。
Tic, x = rand(m,1);Tu = toc tic, x = randn(m,1);Tn = toc比率= tu/ Tn
Tu = 0.3416 tn = 0.4520 ratio = 0.7558因此,随机统一执行时间大约是随机正常执行时间的四分之三。
确认
感谢Peter Perkins在关于MATLAB随机数生成器的整个系列中的帮助。这篇关于金字塔的文章改编自第9.3节MATLAB数值计算.参考文献
George Marsaglia和W. W. Tsang,“一种快速,容易实现的从递减或对称单模密度函数中采样的方法。”SIAM科学与统计计算杂志5, 349-359, 1984。< http://epubs.siam.org/doi/pdf/10.1137/0905026> George Marsaglia和w.w. Tsang,“生成随机变量的金字巨匠方法。”统计软件杂志5,1 - 7,2000。< http://www.jstatsoft.org/v05/i08> Jurgen A. Doornik,“一种改进的Ziggurat方法来生成正常随机样本。”PDF,纳特菲尔德学院,牛津,2005年。< http://www.doornik.com/research/ziggurat.pdfCleve Moler,MATLAB数值计算,暹罗2004年,< http://dx.doi.org/10.1137/1.9780898717952>也可在:<//www.tatmou.com/content/dam/mathworks/mathworks-dot-com/moler/random.pdf>
|














 克利夫角:克利夫莫勒的数学和计算
克利夫角:克利夫莫勒的数学和计算 罗兰谈MATLAB的艺术
罗兰谈MATLAB的艺术 用MATLAB进行图像处理
用MATLAB进行图像处理 Simulin金宝appk上的Guy
Simulin金宝appk上的Guy 深度学习
深度学习 开发区域
开发区域 Stuart的MATLAB视频
Stuart的MATLAB视频 头条新闻背后
头条新闻背后 本周文件交换选择
本周文件交换选择 汉斯谈物联网
汉斯谈物联网 学生休息室
学生休息室 创业公司、加速器和企业家
创业公司、加速器和企业家 MATLAB社区
MATLAB社区 Matlabユザコミュニティ
Matlabユザコミュニティ





评论
如欲留言,请点击在这里登录您的MathWorks帐户或创建一个新帐户。