在1972年一份未发表的技术报告“保护汇流抑制病态”中，Velvel Kahan创造了描述性术语贬义流形.如果你不在日常对话中使用它，贬义的手段“表达蔑视或不同意”。

Velvel的报告关注多项式具有多根，其通常与蔑视认为，因为他们是如此严重制约。但Velvel的重要发现是，虽然多根任意扰动敏感，他们是不敏感的是保持多样性perburbations。同样的观察可以应用到逆矩阵和特征值。

内容

歧管

在这个例子中，带有贬义词的流形$\mathcal{M}$是所有在x = 3处多重数为0的六次多项式的集合。当然，这些都是严格的限制，而且$\mathcal{M}$是所有多项式集合的一个极小子集。但如果我们保持在$ mathcal{M}$范围内，生活就远没有那么残酷了。

两个多项式

首先是一对有多个根的多项式。所有多项式在x = 3处都有一个多重数为3的根以及其他多重根。这个是x = 1处的二重根和x = 2处的单根。

X =符号（'X'）;p1 = (- 3) ^ 3 * (x - 2) * (x - 1) ^ 2;

$$ P1 = {\左（X-1 \右）} ^ 2 \，\左（X-2 \右）\ {\左（X-3 \右）} ^ 3 $$

下一个在x=2时有一个双根，在x=1时有一个单根。

P2 =（X-3）^ 3 *（X-2）^ 2 *（X-1）;

$ $ p2 =左(x - 1 \) \ \{\左(x - 2 \右)}^ 2 \{\左(- 3 \右)}^ 3 $ $

总之，我们有两个多项式，p1和p2．两者都有6次，并且在x = 3处有三重根。此外,pk具有双根在x =K.．

确认

让我们来看看系数。

P1 =扩大（P1）;

$ $ p1 = x ^ 6-13 \, x ^ 5 + 68 \, x ^ 4 - 182 \, x ^ 3 + 261 \, x ^ 2 - 189 \ x + 54 $ $

P2 =扩大（P2）;

$$ P2 = X ^ 6-14 \中，x ^ 5 + 80 \中，x ^ 4-238 \中，x ^ 3 + 387 \中，x ^ 2-324 \中，x + 108 $$

我们可以精确地解出它们并验证它们有想要的根。

z1=解算（p1）'z2=解算（p2）'

Z1 = [1,1,2,3, 3, 3, 3] [1, 2, 2, 3, 3]

凸组合

现在，让我们一凸线性组合。我使用1/3和2/3，但作为它们的和为1。任何这种凸线性组合仍然在$ \ mathcal {M} $我可以使用任何其他的权重为长。

P3 = 1/3*p1 + 2/3*p2;

$ $ p3 = x ^ 6 - \压裂{41 \,x ^ 5} {3} + 76 \, x ^ 4 - \压裂{658 \,x ^ 3} {3} + 345 \, x ^ 2 - 279 \ x + 90 $ $

它在x = 3处仍然有三重根。x = 1和x = 2的根现在是单根x = 5/3的根是1和2的凸线性组合具有相同的系数，5/3 = 1/3*1 + 2/3*2。

z=求解（p3）'

z=[1,5/3,2,3,3,3]

查看三个多项式的曲线图，您可以了解3处的三重根如何比1处的蓝色双根或2处的绿色双根更敏感，而蓝色双根和任何简单根都更敏感。

plot_polys（P1，P2，P3）

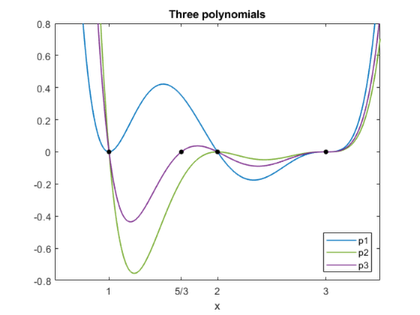
浮点阴霾

现在小perburbation。采取的凸线性组合与不合理的重量和使用VPA中，可变精度浮点运算。我们在一个浮点雾度与厚度$ 10 ^ { - 32} $ $周围\ mathcal {M} $。

数字（32）W = 2 /（1个+ SQRT（VPA（5）））Q = W * P1 +（1-W）* P2;Z = W * 1 +（1-W）* 2

W = 0.61803398874989484820458683436564 Z = 1.3819660112501051517954131656344

这是系数。

disp(多项式系数(q)”)

74.626164607505678196952310944256 -240.56541151876419549238077736064 309.12771741751324912622205886993 -203.39009663000588850054313727552 72.583592135001261821544957987612 -13.381966011250105151795413165634 1.0

找到根源。

Z =解决（q）的

z = 1.0000000000000000000000000000003 1.3819660112501051517954131656331 - 2.0000000000000000000000000000026 3.0000000000990590107064189257617 - 2.9999999999504704946467905371184 2.9999999999504704946467905371184 - 0.000000000085787619734391393745538952850968 + 0.000000000085787619734391393745538952850968我

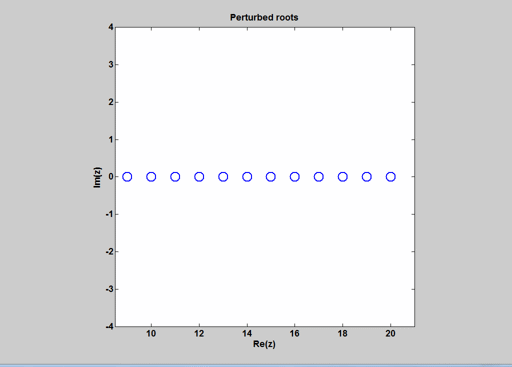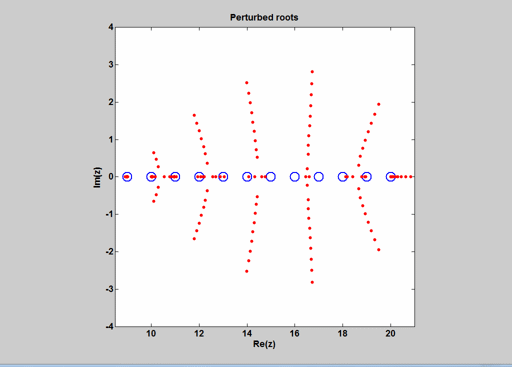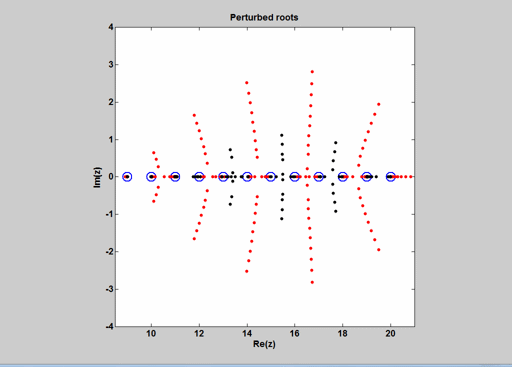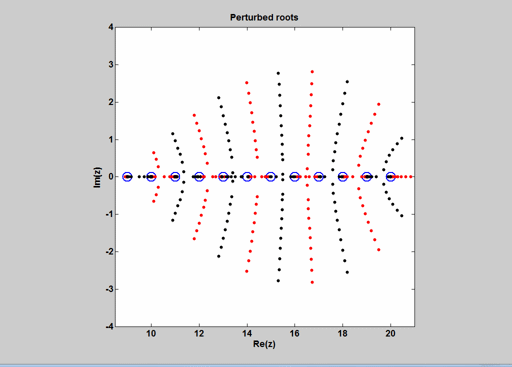
简单的根已经保存到了完全的精度。但是x=3处的三重根被扰动分成了三个复数，位于以x=3为中心的圆上，半径大致等于工作精度的立方根。

圆(双(z (4:6) 3))

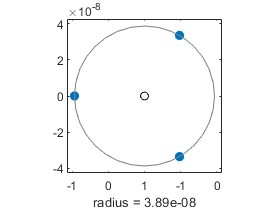
精度的立方根是从哪里来的？我们正试图解这个方程

$$ {\左（X-3 \右）} ^ 3 \，\西格马（X）= 0 $$

其中$\sigma（x）$在$x=3$附近不是零。使用精度为$\epsilon$的浮点运算，我们解决如下问题

$ ${\左(- 3 \右)}^ 3 \ \σ(x) = \ε$ $

解决方案是

左($ $ x = 3 + \ \压裂{\ε}{\σ(x)} \右)^ {1/3}$ $

与立方根承担三个不同的复数值。

双精度

让我们简单地离开符号工具箱。将凸组合中的系数转换为双倍精度，并使用传统的MATLAB函数根．

Q = fliplr（双（coeffs（P3）））';DISP（“q = ')fprintf(“% 25.15 f \ n”，q）格式长Z =根（q）的

q = 1.000000000000000 -13.666666666666666 76.000000000000000 -219.333333333333343 345.000000000000000 -279.000000000000000 90.000000000000000 z = 3.000044739105571 + 0.000077484446947我3.000044739105571 - 0.000077484446947 2.999910521787618 + 0.000000000000000 2.000000000002179 1.666666666665676 + 0.000000000000000 + 0.000000000000000我1.000000000000047 + 0.000000000000000我

这和32位的情况是一样的VPA．在单根X = 1，5/3，和2计算为接近满双精度的精度，而三重根具有精度大致EPS ^（1/3），大约是五位数。

圆（Z（1：3）-3）

冒险离开歧管

从多项式的常数项中减去一个小的量。这将我们移出$\mathcal{M}$。

P = p1 - sym(1.e-4)

P = x^6 - 13*x^5 + 68*x^4 - 182*x^3 + 261*x^2 - 189*x + 539999/10000

我们可以试着精确地找到根，但是修正的多项式不能因式分解有理数。

求解（p）

ans=根（z^6-13*z^5+68*z^4-182*z^3+261*z^2-189*z+539999/10000，z，1）根（z^6-13*z^5+68*z^4-182*z^3+261*z^2-189*z+539999/10000，z，2）根（z^6-13*z^5+68*z^4-182*z^3+261*z^2-189*z+53999/10000，z，3）根（z^6-13*z^5+68*z^4-182*z^3+261*z^2-189*z+539999/10000，z，5）根（z^6-13*z^5+68*z^4-182*z^3+261*z^2-189*z+539999/10000，z，6）

因此，找到根源与数字VPA．这一次所有的根，甚至是简单的根，都受到了影响。

数字（20）Z = VPA（解决（P））

Z = 0.99647996935769229447 1.0035512830254182854 1.9999000099960012995 2.9856883694814744941  -  0.025815296081878984073i 2.9856883694814744941 + 0.025815296081878984073i 3.0286919986579391324

我们建造p1具有在x = 1的双重根，一个简单的根在x = 2，和在x = 3及其multiplicty确定perburbation多少影响它们的三根。

E = abs(double(z - z1'))

E = 0.003520030642308 0.003551283025418 0.000099990003999 0.029516982906352 0.029516982906352 0.028691998657939

未完待续

我提出这个两舞伴。这下一篇文章是关于矩阵的特征值。

关闭

工具书类

中港曾，多项式的故事，PowerPoint演示文稿。>，2003。

W. Kahan的，节约汇合路肩病态。技术报告6，计算机科学，加州大学伯克利分校，1972年。

获取MATLAB代码

发布时间与MATLAB®R2019b

发布时间与MATLAB®R2019b