MathWorks标识,第四部分,特定解决方案的方法生成徽标金宝搏官方网站
特解的方法计算一个高度精确的逼近特征值,我们一直在金宝搏官方网站寻找,并保证精度的界限。它还提供了涉及导致MathWorks徽标的边界条件的灵活性。

 这实际上是l型膜的第一个特征函数。
这实际上是l型膜的第一个特征函数。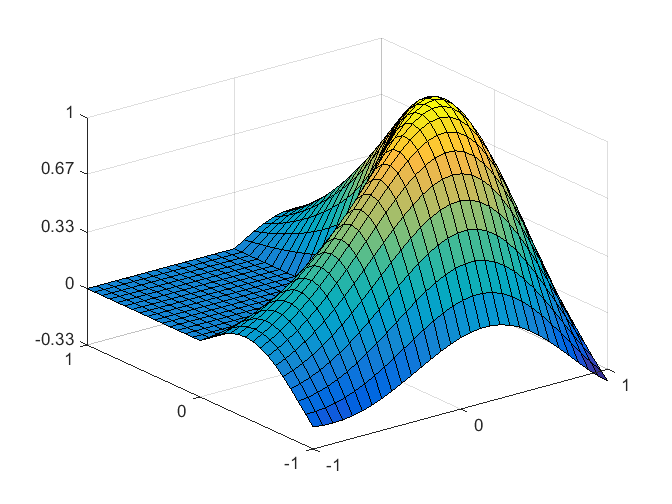 这个函数是偏微分方程$$ u + u = 0 $$的精确解,其值为上面报告的$\lambda$。在可重入角处相交的两条边上满足边界条件$u = 0$,但在外边上明显失效。因此,只有在一定的艺术许可下,我们才可以将其称为l型膜的第一特征函数。当我第一次看到这个的时候冲浪plot,它没有这个华丽的彩色地图,但我发现它的形状很吸引人,所以我把它保留了下来。我下一篇博客的主题是,如何将阴影、灯光和颜色演变成我们的logo。
这个函数是偏微分方程$$ u + u = 0 $$的精确解,其值为上面报告的$\lambda$。在可重入角处相交的两条边上满足边界条件$u = 0$,但在外边上明显失效。因此,只有在一定的艺术许可下,我们才可以将其称为l型膜的第一特征函数。当我第一次看到这个的时候冲浪plot,它没有这个华丽的彩色地图,但我发现它的形状很吸引人,所以我把它保留了下来。我下一篇博客的主题是,如何将阴影、灯光和颜色演变成我们的logo。> Timo Betcke和Lloyd N. Trefethen,复兴特殊解的方法,SIAM Review 47, 469-491, 2005,金宝搏官方网站https://people.maths.ox.ac.uk/trefethen/publication/PDF/2005_112.pdf克里夫硅藻土,MATLAB的数值计算,《偏微分方程》,2004年第11章。<//www.tatmou.com/content/dam/mathworks/mathworks-dot-com/moler/pdes.pdf.>发布了MATLAB®R2014B
内容
Eidgenossische Technische Hochschule苏黎世
1965年至1966年,研究生毕业后,我在苏黎世的瑞士联邦理工学院(ETH)读了一年博士后。当时,该学院的教师包括三位世界著名的数字分析师爱德华·施蒂费尔(Eduard Stiefel)、海因茨·鲁蒂肖泽(Heinz Rutishauser)和彼得·亨里奇(Peter Henrici)。此外,IBM在苏黎世郊区的Ruschlikon有一个研究部门,他们偶尔在那里举行研讨会。10月,牛津大学的莱斯利·福克斯(Leslie Fox)参观了IBM的研究中心,并就他的两个学生琼·沃尔什(Joan Walsh)和约翰·里德(John Reid)在l型薄膜上的工作做了一次演讲。涉及贝塞尔函数的展开式在可重入角附近匹配本征函数的奇异性,在域的其余部分耦合到有限差分网格。在Fox的演讲后不久,我想到了在整个域上使用贝塞尔函数展开并完全避免有限差分。在几周内,我在ETH的CDC 1604主机上进行了计算,这让我非常兴奋。为了庆祝,我用铝箔做了一个l形的装饰品,放在我们公寓的圣诞树上。亨利西提供了一些理论背景,与我正在做的工作,斯蒂芬伯格曼和俄罗斯数学家I. N. Vekua。我们和福克斯一起出版了一篇论文发表在1967年的SIAM数值分析杂志上。特解法金宝搏官方网站
您不需要了解Bessel功能,以欣赏特定解决方案的方法。金宝搏官方网站使用极性坐标,特定解决方案是表单的任何功能$$ v_ \ alpha(\ lambda,r,\ theta)= b_ \ alpha(\ sqrt {\ lambda} r)\ sin {(\ alpha \ theta})首先,请注意$ \ sin {(\ alpha \ theta)} $部分确保此解决方案满足边界条件$$ v_ \ alpha(\ lambda,r,\ theta)= 0 $$沿着两个带有$ \ theta = 0 $和$ \ theta = {\ pi} / {\ alpha} $的光线。对于我们的L形域,重圈角有一定的$ \ frac {3} {2} \ pi $,所以我们希望获得$$ \ alpha = \ frac {2} {3} j $$在哪里$j $是一个整数。Bessel函数$ b_ \ alpha $由普通的微分方程定义,暗示任何$ v_ \ alpha $满足部分微分方程$$ \ delta v_ \ alpha + \ lambda v_ \ alpha = 0 $$ if $ \ alpha $不是一个整数,那么$ b_ \ alpha(r)$有另一个重要的财产。它的衍生品随着$ R $转到0.这种渐近奇点只是我们需要匹配特征功能中的奇点。我们也可以利用对称性。关于L的中心线,第一特征函数是对称的。我们还可以消除来自单位正方形的特征函数的组件。 This implies that for the first eigenfunction $\alpha = \frac{2}{3}j$ where $j$ is an odd integer that is not a multiple of 3, that is $$ \alpha_j = \frac{2}{3}j, \ \ j = 1,5,7,11,13, ... $$边界条件
形成特解的线性组合。金宝搏官方网站$$ u(\lambda,r, theta) = sum_\ c_\ v_\ (\lambda,r, theta) $$这个函数在整个定域内满足我们的微分方程,在可重入角处满足边界条件,并且在那里具有我们想要的奇异行为。所有我们要做的就是选择\λ和美元系数αc_ \美元u美元满足边界条件,u = 0美元,剩下的边缘l .总的想法是选择外边界上的点和研究矩阵获得的评估特定的解决方案在这些点的线性组合。金宝搏官方网站改变$\lambda$直到这个矩阵几乎是缺位的。得到的零向量提供了所需的系数。多年来,我们执行这一总体计划的细节各不相同。最好的方法是在函数中实现membranetx,在这里提供,载于PDE章的MATLAB的数值计算.它使用矩阵计算的主力,SVD,奇异值分解。所涉及矩阵的行数是边界上的点数,列数是和中的项数。下面的数字来自46乘9的矩阵。设$(r_i,\theta_i)$为边界上选择的点。矩阵元素为$$ a_{i,j}(\lambda) = B_{alpha_j}(\sqrt{\lambda} r_i) \sin{(alpha_j \theta_i)} $$fmintx用于改变$\lambda$,并找到该矩阵SVD的最小值。得到的矩阵本质上是缺秩的得到的右奇异向量是一个零向量它提供了系数。最小值是在$$ \lambda = 9.639723844金宝搏官方网站垂直标尺反映了相应系数的大小。mps_figs

所有的四个方面
这四项在外边界上都不接近于零,但当它们加在一起时,图形精度为零。mps_figs(4)
 这实际上是l型膜的第一个特征函数。
这实际上是l型膜的第一个特征函数。只是两个条款
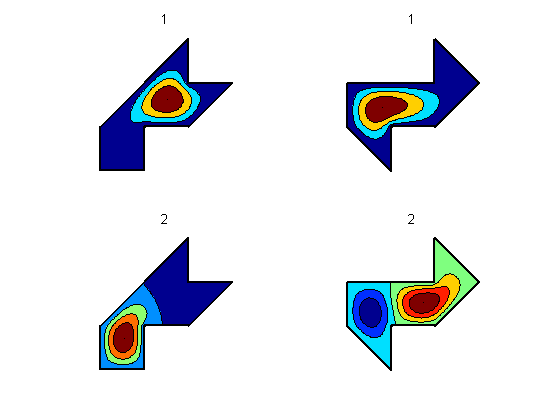
现在我们可以玩得开心。这里有一个冲浪绘制刚是前两个特定解决方案的总和。金宝搏官方网站mps_figs(2)
 这个函数是偏微分方程$$ u + u = 0 $$的精确解,其值为上面报告的$\lambda$。在可重入角处相交的两条边上满足边界条件$u = 0$,但在外边上明显失效。因此,只有在一定的艺术许可下,我们才可以将其称为l型膜的第一特征函数。当我第一次看到这个的时候冲浪plot,它没有这个华丽的彩色地图,但我发现它的形状很吸引人,所以我把它保留了下来。我下一篇博客的主题是,如何将阴影、灯光和颜色演变成我们的logo。
这个函数是偏微分方程$$ u + u = 0 $$的精确解,其值为上面报告的$\lambda$。在可重入角处相交的两条边上满足边界条件$u = 0$,但在外边上明显失效。因此,只有在一定的艺术许可下,我们才可以将其称为l型膜的第一特征函数。当我第一次看到这个的时候冲浪plot,它没有这个华丽的彩色地图,但我发现它的形状很吸引人,所以我把它保留了下来。我下一篇博客的主题是,如何将阴影、灯光和颜色演变成我们的logo。上界和下界
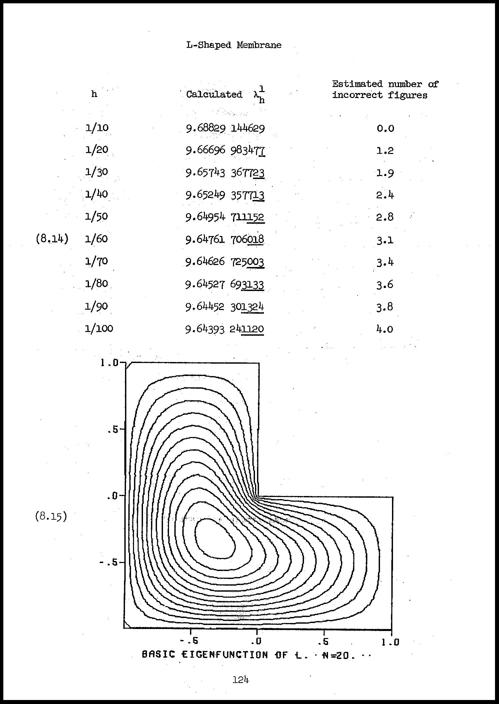
狐狸,henrici和moler纸不仅仅是关于特定解决方案的方法。金宝搏官方网站我们还担心为连续微分算子的确切特征值寻找保证的上限和下限。本文证明的定理涉及与含有特征值的小间隔的宽度达到边缘条件的差异。1966年,我们证明了$ 9.6397238_ {05} <\ lambda <9.6397238 ^ {84} $$membranetx在MATLAB中,我在这个区间的中心找到一个值$\lambda$。(L,λ)= membranetx (1);格式长λ
lambda = 9.639723844021997
特解法的复兴金宝搏官方网站
2005年Timo Betcke和Nick Trefethen发表了一篇论文在暹罗审查指出了我们在Fox, Henrici和Moler论文中描述的方法的一个严重缺陷。当该方法在其他域上尝试时,特别是在有多个奇异角的域上,对于$\lambda$的所有值,矩阵有出现几乎缺秩的趋势。局部极小值很难确定。推荐的解决方法是增加一些内点,并要求近似本征函数在那里是非零的。Betcke和Trefethen还证明了一个近似理论结果,当结合他们的计算时,在第一个特征值的严格边界上又增加了四位数。而且,他们对他们的数值结果是如此的自信,他们确信准确的特征值位于这个区间的中心,他们甚至非常确信他们知道下一位。这与我得到的是一致的membranetx几乎达到全双精度精度。我想我们终于找到了这个家伙。我建议阅读这篇博客的任何人,谁想知道更多关于特殊解的方法和计算的特征值的l形膜阅读金宝搏官方网站Betcke和Trefethen纸.参考文献
Leslie Fox, Peter Henrici,和Cleve Moler,椭圆算子特征值的逼近和界限,SIAM数值分析4,89-102,1967,
|














 克利夫角:克利夫·莫尔谈数学和计算机
克利夫角:克利夫·莫尔谈数学和计算机 Loren在Matlab的艺术上
Loren在Matlab的艺术上 史蒂夫在图像处理与matlab
史蒂夫在图像处理与matlab 人在仿真软件金宝app
人在仿真软件金宝app 深度学习
深度学习 开发区域
开发区域 Stuart的Matlab视频
Stuart的Matlab视频 在头条新闻后面
在头条新闻后面 本周的文件交换选择
本周的文件交换选择 汉斯在物联网
汉斯在物联网 学生休息室
学生休息室 初创企业、加速器和企业家
初创企业、加速器和企业家 MATLAB社区
MATLAB社区 MATLABユーザーコミュニティー
MATLABユーザーコミュニティー



评论
要发表评论,请点击在这里要登录您的MathWorks帐户或创建新的。