性能考虑- MATLAB和Simulink金宝app - 金宝app,下载188bet金宝搏,金宝搏官方网站

性能考虑

管理内存

在解决SDE引擎支持的大多数问题时，有两种常用的内存管理方法:金宝app

使用输出管理内存

执行传统模拟来模拟感兴趣的底层变量，特别是请求并操作输出数组。

这种方法简单明了，是小型或中型问题的最佳选择。由于它的输出是数组，便于在MATLAB中操纵仿真结果^®依赖于语言。但是，随着问题规模的增加，这种方法的好处就会减少，因为输出数组必须存储大量可能无关的信息。

例如，考虑为一个欧洲期权定价，其中标的资产的终端价格是唯一的利息价值。为了减轻传统方法的内存负担，可以减少由所需输入指定的模拟周期的数量NPeriods并指定可选输入NSteps．这使您能够在不牺牲准确性的情况下管理内存(参见优化精度:关于解的精度和误差）.

此外，仿真方法可以确定输出参数的数量，并相应地分配内存。具体来说，所有的模拟方法都支持相同的输出参数列表:金宝app

(Z路径、时间)

在哪里路径和Z可以是大的、三维的时间序列阵列。然而，底层噪声数组通常是不必要的，并且只有在请求作为输出时才存储。换句话说,Z仅在您要求时存储;如果你不需要它，不要要求它。

如果你需要输出噪声阵列Z，但不需要路径时间序列数组，则可避免存储路径两种方式:

最好的做法是使用～输出参数占位符。例如，使用下面的输出参数列表进行存储Z和次,但不路径：
```
(~,, Z)
```
使用可选的输入标志路径，所有的仿真方法都支持。金宝app默认情况下,路径存储(路径＝真正的）.然而,设置路径来假返回路径作为一个空矩阵。

使用周期结束处理函数管理内存

指定一个或多个周期结束处理函数来仅管理和存储感兴趣的信息，避免全部模拟输出。

这种方法要求您指定一个或多个周期结束处理函数，并且通常是大规模问题的首选方法。这种方法允许您完全避免模拟输出。由于没有输出要求，三维时间序列阵列路径和Z不存储。

这种方法通常需要更多的工作，但是更加优雅，允许您自定义任务并显著减少内存使用。看到股票期权定价．

提高性能

在解决SDE问题时，以下方法可以提高性能:

指定模型参数作为传统的MATLAB数组和函数，在各种组合。这提供了一个灵活的接口，可以支持几乎任何一般的非线性关系。金宝app然而，虽然函数为许多问题提供了方便和优雅的解决方案，但当您将参数指定为双精度向量或矩阵时，模拟通常运行得更快。因此，如果可能，最好将模型参数指定为数组。
如果可能，使用重载欧拉模拟方法的模型。利用布朗运动(BM)和几何布朗运动(“绿带运动”)模型，提供重载的欧拉仿真方法，利用可分离的，常数参数模型。这些专门的方法非常快，但只对具有常数参数的模型可用，而不指定周期结束处理和噪声生成函数。
代替模拟的一个常数参数，由一元模型推导而来SDEDDO类与对角线多元模型．将多元模型视为单变量模型的组合。这增加了模型的维数，并通过减少模拟试验的有效次数来提高性能。

请注意

该技术仅适用于常参数单变量模型，不指定周期结束处理和噪声产生函数。
利用仿真方法被设计来检测存在的事实南(不是数字)条件从周期结束处理函数返回。一个南表示未定义数值计算的结果，以及基于南产生另一个南．这有助于在某些情况下提高性能。例如，考虑模拟淘汰障碍期权(也就是说，当标的资产的价格越过某些规定的障碍时，该期权就变得毫无价值)的底层期权的路径。你的句号结束函数可以检测障碍穿越并返回南以提前结束目前的审判。

优化精度:关于解的精度和误差

模拟体系结构通常不进行模拟确切的金宝搏官方网站任何SDE的解决方案。相反，模拟体系结构提供了底层连续时间过程的离散时间近似，这种模拟技术通常被称为欧拉近似．

在大多数情况下，给定的模拟直接从SDE派生。因此，模拟的离散过程仅在时间增量的极限下接近底层的连续过程dt接近零。换句话说，仿真体系结构更重视确保离散时间和连续时间过程的概率分布是相近的，而不是过程的路径接近。

在说明改进解的近似方法之前，先了解误差的来源是有帮助的。金宝搏官方网站在整个体系结构中，所有仿真方法都假定模型参数在任何时间间隔内都是分段常数dt．事实上，这些方法甚至在每个时间间隔开始时评估动态参数，并在间隔的持续时间内保持它们固定。这种抽样方法介绍了离散化误差．

然而，对于某些模型，分段常数法提供了精确的解:金宝搏官方网站

创建布朗运动(BM)模型，采用欧拉近似(simByEuler）.
创建几何布朗运动(GBM)模型参数不变，用封闭解(simBySolution）.
创建Hull-White/Vasicek (HWV)高斯扩散模型参数不变，用封闭解(simBySolution）

更一般地说，即使参数随时间变化，你也可以模拟这些模型的精确解，如果它们以一种分段常数的金宝搏官方网站方式变化，使参数的变化与指定的采样时间一致。然而，这种确切的巧合是不可能的;因此，前面讨论的常数参数条件在实践中是常用的。

提高精度的一个明显方法是更频繁地对离散时间过程进行采样。这将减少时间增量(dt)，使得采样过程更接近底层的连续时间过程。尽管减少时间增量是普遍适用的，但是，在准确性、运行时性能和内存使用之间存在权衡。

要管理这种折衷，请指定一个可选的输入参数，NSteps，用于所有仿真方法。NSteps指示每个时间增量内的中间时间步长的数目dt，在那里对过程进行抽样但不报告。

在这一点上，强调输入的关系是重要且方便的NSteps，NPeriods,DeltaTime到输出向量次，表示模拟路径报告时的实际观测时间。

NPeriods，表示所需输入的仿真周期长度DeltaTime，并确定模拟三维空间中的行数路径时间序列数组(如果请求输出)。
DeltaTime为可选，表示对应的NPeriods连续样本之间正时间增量的长度向量。它代表熟悉的事物dt在随机微分方程中。如果DeltaTime时，使用默认值1。
NSteps也是可选的，并且只与NPeriods和DeltaTime．NSteps指定每个时间增量内的中间时间步长的数目DeltaTime．
具体来说，每次时间都在增加DeltaTime被划分到NSteps小区间的长度DeltaTime/NSteps，并通过计算仿真状态向量来细化仿真(NSteps - 1)中间时期。虽然输出状态向量(如果请求)在这些中间时间没有被报告，但是这种改进通过使模拟更接近底层连续时间过程来提高精度。如果NSteps时，默认值为1(表示无中间评估)。
输出次是一个NPeriods + 1-与模拟路径相关联的观测时间的长度列向量。的每个元素次与相应的路径．

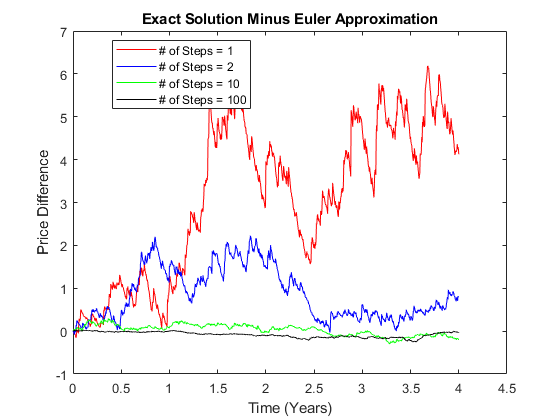
下面的例子通过比较封闭解和由不同的值导出的欧拉近似序列之间的差异来说明这种中间采样NSteps．

例如:提高解决方案的准确性

考虑一个单变量几何布朗运动(“绿带运动”)模型使用“绿带运动”在恒定的参数:

$d X_{t} ＝ 0．1 X_{t} d t + 0．4 X_{t} d W_{t} ．$

假设预期收益率和波动率参数是按年计算的，一个日历年包括250个交易日。

模拟大约四年的单变量价格的精确解和欧拉逼近的各种值NSteps：

nPeriods = 1000;dt = 1/250;obj =“绿带运动”(0.1,0.4,“StartState”, 100);rng (575“旋风”) [X1,T1] = simBySolution(obj,nPeriods，“DeltaTime”, dt);rng (575“旋风”) [Y1,T1] = simByEuler(obj,nPeriods，“DeltaTime”, dt);rng (575“旋风”) [X2,T2] = simBySolution(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”2);rng (575“旋风”) [Y2,T2] = simByEuler(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”2);rng (575“旋风”) [X3,T3] = simBySolution(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”10);rng (575“旋风”) [Y3,T3] = simByEuler(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”10);rng (575“旋风”) [X4,T4] = simBySolution(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”, 100);rng (575“旋风”) [Y4,T4] = simByEuler(obj,nPeriods，“DeltaTime”，．..dt,“nSteps”, 100);

用图形来比较误差(精确解和欧拉近似之间的差异):

clf;情节(T1, X1 - Y1,“红色”)举行在；情节(T2, X2, Y2,“蓝”图(T3,X3 - Y3，“绿色”)图(T4,X4 - Y4，“黑”)举行从包含(的时间(年)) ylabel (“差价”)标题(“精确解减去欧拉近似”)({传奇'# of Steps = 1''# of Steps = 2'．..'# of Steps = 10''# of Steps = 100'}，．..“位置”，“最佳”)举行从

谁TXY

正如预期的那样，模拟误差随着中间时间步长的增加而减小。由于没有报告中间状态，所以所有模拟时间序列的观测值都是相同的，而不管实际值是多少NSteps．

此外，由于前面模拟的精确解对于任何数量的中间时间步骤都是正确的，因此本例不需要额外的计算。金宝搏官方网站事实上，这种评价是正确的。在中间时刻对精确解进金宝搏官方网站行采样，以确保模拟使用相同顺序的高斯随机变量序列。没有这种保证，就没有办法在路径基础上比较模拟价格。然而，可能有正当的理由在紧密的间隔时间内抽样精确的解决方案，如定价路径依赖的选项。金宝搏官方网站